Base class for all dense matrices, vectors, and expressions. More...

#include <MatrixBase.h>

Inheritance diagram for MatrixBase< Derived >:

Classes
struct	ConstDiagonalIndexReturnType
struct	ConstSelfAdjointViewReturnType
struct	ConstTriangularViewReturnType
struct	cross_product_return_type
struct	DiagonalIndexReturnType
struct	SelfAdjointViewReturnType
struct	TriangularViewReturnType
Public Types
enum	{ SizeMinusOne = SizeAtCompileTime==Dynamic ? Dynamic : SizeAtCompileTime-1 }
typedef MatrixBase	StorageBaseType
typedef internal::traits < Derived >::StorageKind	StorageKind
typedef internal::traits < Derived >::Index	Index
typedef internal::traits < Derived >::Scalar	Scalar
typedef internal::packet_traits < Scalar >::type	PacketScalar
typedef NumTraits< Scalar >::Real	RealScalar
typedef DenseBase< Derived >	Base
typedef Base::CoeffReturnType	CoeffReturnType
typedef Base::ConstTransposeReturnType	ConstTransposeReturnType
typedef Base::RowXpr	RowXpr
typedef Base::ColXpr	ColXpr
typedef Matrix< Scalar, EIGEN_SIZE_MAX(RowsAtCompileTime, ColsAtCompileTime), EIGEN_SIZE_MAX(RowsAtCompileTime, ColsAtCompileTime)>	SquareMatrixType
typedef Matrix< typename internal::traits< Derived > ::Scalar, internal::traits < Derived >::RowsAtCompileTime, internal::traits< Derived > ::ColsAtCompileTime, AutoAlign\|(internal::traits < Derived >::Flags &RowMajorBit?RowMajor:ColMajor), internal::traits< Derived > ::MaxRowsAtCompileTime, internal::traits< Derived > ::MaxColsAtCompileTime >	PlainObject
	The plain matrix type corresponding to this expression.
typedef CwiseNullaryOp < internal::scalar_constant_op < Scalar >, Derived >	ConstantReturnType
typedef internal::conditional < NumTraits< Scalar > ::IsComplex, CwiseUnaryOp < internal::scalar_conjugate_op < Scalar > , ConstTransposeReturnType > , ConstTransposeReturnType > ::type	AdjointReturnType
typedef Matrix< std::complex < RealScalar > , internal::traits< Derived > ::ColsAtCompileTime, 1, ColMajor >	EigenvaluesReturnType
typedef CwiseNullaryOp < internal::scalar_identity_op < Scalar >, Derived >	IdentityReturnType
typedef Block< const CwiseNullaryOp < internal::scalar_identity_op < Scalar >, SquareMatrixType > , internal::traits< Derived > ::RowsAtCompileTime, internal::traits< Derived > ::ColsAtCompileTime >	BasisReturnType
typedef CwiseUnaryOp < internal::scalar_multiple_op < Scalar >, const Derived >	ScalarMultipleReturnType
typedef CwiseUnaryOp < internal::scalar_quotient1_op < Scalar >, const Derived >	ScalarQuotient1ReturnType
typedef internal::conditional < NumTraits< Scalar > ::IsComplex, const CwiseUnaryOp < internal::scalar_conjugate_op < Scalar >, const Derived > , const Derived & >::type	ConjugateReturnType
typedef internal::conditional < NumTraits< Scalar > ::IsComplex, const CwiseUnaryOp < internal::scalar_real_op < Scalar >, const Derived > , const Derived & >::type	RealReturnType
typedef internal::conditional < NumTraits< Scalar > ::IsComplex, CwiseUnaryView < internal::scalar_real_ref_op < Scalar >, Derived >, Derived & > ::type	NonConstRealReturnType
typedef CwiseUnaryOp < internal::scalar_imag_op < Scalar >, const Derived >	ImagReturnType
typedef CwiseUnaryView < internal::scalar_imag_ref_op < Scalar >, Derived >	NonConstImagReturnType
typedef Diagonal< Derived >	DiagonalReturnType
typedef const Diagonal< const Derived >	ConstDiagonalReturnType
typedef Block< const Derived, internal::traits< Derived > ::ColsAtCompileTime==1?SizeMinusOne:1, internal::traits< Derived > ::ColsAtCompileTime==1?1:SizeMinusOne >	ConstStartMinusOne
typedef CwiseUnaryOp < internal::scalar_quotient1_op < typename internal::traits < Derived >::Scalar >, const ConstStartMinusOne >	HNormalizedReturnType
typedef internal::stem_function < Scalar >::type	StemFunction
Public Member Functions
Index	diagonalSize () const
const CwiseUnaryOp < internal::scalar_opposite_op < typename internal::traits < Derived >::Scalar >, const Derived >	operator- () const
const ScalarMultipleReturnType	operator* (const Scalar &scalar) const
const CwiseUnaryOp < internal::scalar_quotient1_op < typename internal::traits < Derived >::Scalar >, const Derived >	operator/ (const Scalar &scalar) const
const CwiseUnaryOp < internal::scalar_multiple2_op < Scalar, std::complex< Scalar > >, const Derived >	operator* (const std::complex< Scalar > &scalar) const
template<typename NewType >
internal::cast_return_type < Derived, const CwiseUnaryOp < internal::scalar_cast_op < typename internal::traits < Derived >::Scalar, NewType > , const Derived > >::type	cast () const
ConjugateReturnType	conjugate () const
RealReturnType	real () const
const ImagReturnType	imag () const
template<typename CustomUnaryOp >
const CwiseUnaryOp < CustomUnaryOp, const Derived >	unaryExpr (const CustomUnaryOp &func=CustomUnaryOp()) const
	Apply a unary operator coefficient-wise.
template<typename CustomViewOp >
const CwiseUnaryView < CustomViewOp, const Derived >	unaryViewExpr (const CustomViewOp &func=CustomViewOp()) const
NonConstRealReturnType	real ()
NonConstImagReturnType	imag ()
template<typename CustomBinaryOp , typename OtherDerived >
EIGEN_STRONG_INLINE const CwiseBinaryOp< CustomBinaryOp, const Derived, const OtherDerived >	binaryExpr (const EIGEN_CURRENT_STORAGE_BASE_CLASS< OtherDerived > &other, const CustomBinaryOp &func=CustomBinaryOp()) const
EIGEN_STRONG_INLINE const CwiseUnaryOp < internal::scalar_abs_op < Scalar >, const Derived >	cwiseAbs () const
EIGEN_STRONG_INLINE const CwiseUnaryOp < internal::scalar_abs2_op < Scalar >, const Derived >	cwiseAbs2 () const
const CwiseUnaryOp < internal::scalar_sqrt_op < Scalar >, const Derived >	cwiseSqrt () const
const CwiseUnaryOp < internal::scalar_inverse_op < Scalar >, const Derived >	cwiseInverse () const
const CwiseUnaryOp < std::binder1st < std::equal_to< Scalar > >, const Derived >	cwiseEqual (const Scalar &s) const
template<typename OtherDerived >
EIGEN_STRONG_INLINE const	EIGEN_CWISE_PRODUCT_RETURN_TYPE (Derived, OtherDerived) cwiseProduct(const EIGEN_CURRENT_STORAGE_BASE_CLASS< OtherDerived > &other) const
template<typename OtherDerived >
const CwiseBinaryOp < std::equal_to< Scalar > , const Derived, const OtherDerived >	cwiseEqual (const EIGEN_CURRENT_STORAGE_BASE_CLASS< OtherDerived > &other) const
template<typename OtherDerived >
const CwiseBinaryOp < std::not_equal_to< Scalar > , const Derived, const OtherDerived >	cwiseNotEqual (const EIGEN_CURRENT_STORAGE_BASE_CLASS< OtherDerived > &other) const
template<typename OtherDerived >
EIGEN_STRONG_INLINE const CwiseBinaryOp < internal::scalar_min_op < Scalar >, const Derived, const OtherDerived >	cwiseMin (const EIGEN_CURRENT_STORAGE_BASE_CLASS< OtherDerived > &other) const
template<typename OtherDerived >
EIGEN_STRONG_INLINE const CwiseBinaryOp < internal::scalar_max_op < Scalar >, const Derived, const OtherDerived >	cwiseMax (const EIGEN_CURRENT_STORAGE_BASE_CLASS< OtherDerived > &other) const
template<typename OtherDerived >
EIGEN_STRONG_INLINE const CwiseBinaryOp < internal::scalar_quotient_op < Scalar >, const Derived, const OtherDerived >	cwiseQuotient (const EIGEN_CURRENT_STORAGE_BASE_CLASS< OtherDerived > &other) const
Derived &	operator= (const MatrixBase &other)
template<typename OtherDerived >
Derived &	operator= (const DenseBase< OtherDerived > &other)
template<typename OtherDerived >
Derived &	operator= (const EigenBase< OtherDerived > &other)
	Copies the generic expression other into *this.
template<typename OtherDerived >
Derived &	operator= (const ReturnByValue< OtherDerived > &other)
template<typename ProductDerived , typename Lhs , typename Rhs >
Derived &	lazyAssign (const ProductBase< ProductDerived, Lhs, Rhs > &other)
template<typename OtherDerived >
Derived &	operator+= (const MatrixBase< OtherDerived > &other)
template<typename OtherDerived >
Derived &	operator-= (const MatrixBase< OtherDerived > &other)
template<typename OtherDerived >
const ProductReturnType < Derived, OtherDerived > ::Type	operator* (const MatrixBase< OtherDerived > &other) const
template<typename OtherDerived >
const LazyProductReturnType < Derived, OtherDerived > ::Type	lazyProduct (const MatrixBase< OtherDerived > &other) const
template<typename OtherDerived >
Derived &	operator*= (const EigenBase< OtherDerived > &other)
template<typename OtherDerived >
void	applyOnTheLeft (const EigenBase< OtherDerived > &other)
template<typename OtherDerived >
void	applyOnTheRight (const EigenBase< OtherDerived > &other)
template<typename DiagonalDerived >
const DiagonalProduct< Derived, DiagonalDerived, OnTheRight >	operator* (const DiagonalBase< DiagonalDerived > &diagonal) const
template<typename OtherDerived >
internal::scalar_product_traits < typename internal::traits < Derived >::Scalar, typename internal::traits< OtherDerived > ::Scalar >::ReturnType	dot (const MatrixBase< OtherDerived > &other) const
RealScalar	squaredNorm () const
RealScalar	norm () const
RealScalar	stableNorm () const
RealScalar	blueNorm () const
RealScalar	hypotNorm () const
const PlainObject	normalized () const
void	normalize ()
const AdjointReturnType	adjoint () const
void	adjointInPlace ()
DiagonalReturnType	diagonal ()
const ConstDiagonalReturnType	diagonal () const
template<int Index>
DiagonalIndexReturnType< Index > ::Type	diagonal ()
template<int Index>
ConstDiagonalIndexReturnType < Index >::Type	diagonal () const
DiagonalIndexReturnType < Dynamic >::Type	diagonal (Index index)
ConstDiagonalIndexReturnType < Dynamic >::Type	diagonal (Index index) const
template<unsigned int Mode>
TriangularViewReturnType< Mode > ::Type	triangularView ()
template<unsigned int Mode>
ConstTriangularViewReturnType < Mode >::Type	triangularView () const
template<unsigned int UpLo>
SelfAdjointViewReturnType < UpLo >::Type	selfadjointView ()
template<unsigned int UpLo>
ConstSelfAdjointViewReturnType < UpLo >::Type	selfadjointView () const
const SparseView< Derived >	sparseView (const Scalar &m_reference=Scalar(0), typename NumTraits< Scalar >::Real m_epsilon=NumTraits< Scalar >::dummy_precision()) const
const DiagonalWrapper< const Derived >	asDiagonal () const
const PermutationWrapper < const Derived >	asPermutation () const
Derived &	setIdentity ()
Derived &	setIdentity (Index rows, Index cols)
	Resizes to the given size, and writes the identity expression (not necessarily square) into *this.
bool	isIdentity (RealScalar prec=NumTraits< Scalar >::dummy_precision()) const
bool	isDiagonal (RealScalar prec=NumTraits< Scalar >::dummy_precision()) const
bool	isUpperTriangular (RealScalar prec=NumTraits< Scalar >::dummy_precision()) const
bool	isLowerTriangular (RealScalar prec=NumTraits< Scalar >::dummy_precision()) const
template<typename OtherDerived >
bool	isOrthogonal (const MatrixBase< OtherDerived > &other, RealScalar prec=NumTraits< Scalar >::dummy_precision()) const
bool	isUnitary (RealScalar prec=NumTraits< Scalar >::dummy_precision()) const
template<typename OtherDerived >
bool	operator== (const MatrixBase< OtherDerived > &other) const
template<typename OtherDerived >
bool	operator!= (const MatrixBase< OtherDerived > &other) const
NoAlias< Derived, Eigen::MatrixBase >	noalias ()
const ForceAlignedAccess< Derived >	forceAlignedAccess () const
ForceAlignedAccess< Derived >	forceAlignedAccess ()
template<bool Enable>
internal::add_const_on_value_type < typename internal::conditional< Enable, ForceAlignedAccess< Derived > , Derived & >::type >::type	forceAlignedAccessIf () const
template<bool Enable>
internal::conditional< Enable, ForceAlignedAccess< Derived > , Derived & >::type	forceAlignedAccessIf ()
Scalar	trace () const
template<int p>
RealScalar	lpNorm () const
MatrixBase< Derived > &	matrix ()
const MatrixBase< Derived > &	matrix () const
ArrayWrapper< Derived >	array ()
const ArrayWrapper< Derived >	array () const
const FullPivLU< PlainObject >	fullPivLu () const
const PartialPivLU< PlainObject >	partialPivLu () const
const internal::inverse_impl < Derived >	inverse () const
template<typename ResultType >
void	computeInverseAndDetWithCheck (ResultType &inverse, typename ResultType::Scalar &determinant, bool &invertible, const RealScalar &absDeterminantThreshold=NumTraits< Scalar >::dummy_precision()) const
template<typename ResultType >
void	computeInverseWithCheck (ResultType &inverse, bool &invertible, const RealScalar &absDeterminantThreshold=NumTraits< Scalar >::dummy_precision()) const
Scalar	determinant () const
const LLT< PlainObject >	llt () const
const LDLT< PlainObject >	ldlt () const
const HouseholderQR< PlainObject >	householderQr () const
const ColPivHouseholderQR < PlainObject >	colPivHouseholderQr () const
const FullPivHouseholderQR < PlainObject >	fullPivHouseholderQr () const
EigenvaluesReturnType	eigenvalues () const
	Computes the eigenvalues of a matrix.
RealScalar	operatorNorm () const
	Computes the L2 operator norm.
JacobiSVD< PlainObject >	jacobiSvd (unsigned int computationOptions=0) const
template<typename OtherDerived >
cross_product_return_type < OtherDerived >::type	cross (const MatrixBase< OtherDerived > &other) const
template<typename OtherDerived >
PlainObject	cross3 (const MatrixBase< OtherDerived > &other) const
PlainObject	unitOrthogonal (void) const
Matrix< Scalar, 3, 1 >	eulerAngles (Index a0, Index a1, Index a2) const
const HNormalizedReturnType	hnormalized () const
void	makeHouseholderInPlace (Scalar &tau, RealScalar &beta)
template<typename EssentialPart >
void	makeHouseholder (EssentialPart &essential, Scalar &tau, RealScalar &beta) const
template<typename EssentialPart >
void	applyHouseholderOnTheLeft (const EssentialPart &essential, const Scalar &tau, Scalar *workspace)
template<typename EssentialPart >
void	applyHouseholderOnTheRight (const EssentialPart &essential, const Scalar &tau, Scalar *workspace)
template<typename OtherScalar >
void	applyOnTheLeft (Index p, Index q, const JacobiRotation< OtherScalar > &j)
template<typename OtherScalar >
void	applyOnTheRight (Index p, Index q, const JacobiRotation< OtherScalar > &j)
const MatrixExponentialReturnValue < Derived >	exp () const
const MatrixFunctionReturnValue < Derived >	matrixFunction (StemFunction f) const
const MatrixFunctionReturnValue < Derived >	cosh () const
const MatrixFunctionReturnValue < Derived >	sinh () const
const MatrixFunctionReturnValue < Derived >	cos () const
const MatrixFunctionReturnValue < Derived >	sin () const
template<typename Derived >
MatrixBase< Derived > ::ScalarMultipleReturnType	operator* (const UniformScaling< Scalar > &s) const
Static Public Member Functions
static const IdentityReturnType	Identity ()
static const IdentityReturnType	Identity (Index rows, Index cols)
static const BasisReturnType	Unit (Index size, Index i)
static const BasisReturnType	Unit (Index i)
static const BasisReturnType	UnitX ()
static const BasisReturnType	UnitY ()
static const BasisReturnType	UnitZ ()
static const BasisReturnType	UnitW ()
Protected Member Functions
	MatrixBase ()
template<typename OtherDerived >
Derived &	operator+= (const ArrayBase< OtherDerived > &)
template<typename OtherDerived >
Derived &	operator-= (const ArrayBase< OtherDerived > &)
Friends
const ScalarMultipleReturnType	operator* (const Scalar &scalar, const StorageBaseType &matrix)
const CwiseUnaryOp < internal::scalar_multiple2_op < Scalar, std::complex< Scalar > >, const Derived >	operator* (const std::complex< Scalar > &scalar, const StorageBaseType &matrix)

Detailed Description

template<typename Derived>
class MatrixBase< Derived >

Base class for all dense matrices, vectors, and expressions.

This class is the base that is inherited by all matrix, vector, and related expression types. Most of the Eigen API is contained in this class, and its base classes. Other important classes for the Eigen API are Matrix, and VectorwiseOp.

Note that some methods are defined in other modules such as the LU_Module LU module for all functions related to matrix inversions.

Template Parameters:

Derived

is the derived type, e.g. a matrix type, or an expression, etc.

When writing a function taking Eigen objects as argument, if you want your function to take as argument any matrix, vector, or expression, just let it take a MatrixBase argument. As an example, here is a function printFirstRow which, given a matrix, vector, or expression x, prints the first row of x.

    template<typename Derived>
    void printFirstRow(const Eigen::MatrixBase<Derived>& x)
    {
      cout << x.row(0) << endl;
    }

This class can be extended with the help of the plugin mechanism described on the page TopicCustomizingEigen by defining the preprocessor symbol EIGEN_MATRIXBASE_PLUGIN.

See also:: TopicClassHierarchy

Member Typedef Documentation

template<typename Derived>

typedef internal::conditional<NumTraits<Scalar>::IsComplex, CwiseUnaryOp<internal::scalar_conjugate_op<Scalar>, ConstTransposeReturnType>, ConstTransposeReturnType >::type MatrixBase< Derived >::AdjointReturnType

template<typename Derived>

typedef DenseBase<Derived> MatrixBase< Derived >::Base

Reimplemented from DenseBase< Derived >.

template<typename Derived>

typedef Block<const CwiseNullaryOp<internal::scalar_identity_op<Scalar>, SquareMatrixType>, internal::traits<Derived>::RowsAtCompileTime, internal::traits<Derived>::ColsAtCompileTime> MatrixBase< Derived >::BasisReturnType

template<typename Derived>

typedef Base::CoeffReturnType MatrixBase< Derived >::CoeffReturnType

Reimplemented from DenseBase< Derived >.

template<typename Derived>

typedef Base::ColXpr MatrixBase< Derived >::ColXpr

Reimplemented from DenseBase< Derived >.

template<typename Derived>

typedef internal::conditional<NumTraits<Scalar>::IsComplex, const CwiseUnaryOp<internal::scalar_conjugate_op<Scalar>, const Derived>, const Derived& >::type MatrixBase< Derived >::ConjugateReturnType

template<typename Derived>

typedef CwiseNullaryOp<internal::scalar_constant_op<Scalar>,Derived> MatrixBase< Derived >::ConstantReturnType

Reimplemented from DenseBase< Derived >.

template<typename Derived>

typedef const Diagonal<const Derived> MatrixBase< Derived >::ConstDiagonalReturnType

template<typename Derived>

typedef Block<const Derived, internal::traits<Derived>::ColsAtCompileTime==1 ? SizeMinusOne : 1, internal::traits<Derived>::ColsAtCompileTime==1 ? 1 : SizeMinusOne> MatrixBase< Derived >::ConstStartMinusOne

template<typename Derived>

typedef Base::ConstTransposeReturnType MatrixBase< Derived >::ConstTransposeReturnType

Reimplemented from DenseBase< Derived >.

template<typename Derived>

typedef Diagonal<Derived> MatrixBase< Derived >::DiagonalReturnType

template<typename Derived>

typedef Matrix<std::complex<RealScalar>, internal::traits<Derived>::ColsAtCompileTime, 1, ColMajor> MatrixBase< Derived >::EigenvaluesReturnType

Reimplemented from DenseBase< Derived >.

template<typename Derived>

typedef CwiseUnaryOp<internal::scalar_quotient1_op<typename internal::traits<Derived>::Scalar>, const ConstStartMinusOne > MatrixBase< Derived >::HNormalizedReturnType

template<typename Derived>

typedef CwiseNullaryOp<internal::scalar_identity_op<Scalar>,Derived> MatrixBase< Derived >::IdentityReturnType

template<typename Derived>

typedef CwiseUnaryOp<internal::scalar_imag_op<Scalar>, const Derived> MatrixBase< Derived >::ImagReturnType

template<typename Derived>

typedef internal::traits<Derived>::Index MatrixBase< Derived >::Index

The type of indices

Reimplemented from DenseBase< Derived >.

template<typename Derived>

typedef CwiseUnaryView<internal::scalar_imag_ref_op<Scalar>, Derived> MatrixBase< Derived >::NonConstImagReturnType

template<typename Derived>

typedef internal::conditional<NumTraits<Scalar>::IsComplex, CwiseUnaryView<internal::scalar_real_ref_op<Scalar>, Derived>, Derived& >::type MatrixBase< Derived >::NonConstRealReturnType

template<typename Derived>

typedef internal::packet_traits<Scalar>::type MatrixBase< Derived >::PacketScalar

Reimplemented from DenseBase< Derived >.

template<typename Derived>

typedef Matrix<typename internal::traits<Derived>::Scalar, internal::traits<Derived>::RowsAtCompileTime, internal::traits<Derived>::ColsAtCompileTime, AutoAlign | (internal::traits<Derived>::Flags&RowMajorBit ? RowMajor : ColMajor), internal::traits<Derived>::MaxRowsAtCompileTime, internal::traits<Derived>::MaxColsAtCompileTime > MatrixBase< Derived >::PlainObject

The plain matrix type corresponding to this expression.

This is not necessarily exactly the return type of eval(). In the case of plain matrices, the return type of eval() is a const reference to a matrix, not a matrix! It is however guaranteed that the return type of eval() is either PlainObject or const PlainObject&.

template<typename Derived>

typedef internal::conditional<NumTraits<Scalar>::IsComplex, const CwiseUnaryOp<internal::scalar_real_op<Scalar>, const Derived>, const Derived& >::type MatrixBase< Derived >::RealReturnType

template<typename Derived>

typedef NumTraits<Scalar>::Real MatrixBase< Derived >::RealScalar

Reimplemented from DenseBase< Derived >.

template<typename Derived>

typedef Base::RowXpr MatrixBase< Derived >::RowXpr

Reimplemented from DenseBase< Derived >.

template<typename Derived>

typedef internal::traits<Derived>::Scalar MatrixBase< Derived >::Scalar

Reimplemented from DenseBase< Derived >.

Reimplemented in ScaledProduct< NestedProduct >.

template<typename Derived>

typedef CwiseUnaryOp<internal::scalar_multiple_op<Scalar>, const Derived> MatrixBase< Derived >::ScalarMultipleReturnType

template<typename Derived>

typedef CwiseUnaryOp<internal::scalar_quotient1_op<Scalar>, const Derived> MatrixBase< Derived >::ScalarQuotient1ReturnType

template<typename Derived>

typedef Matrix<Scalar,EIGEN_SIZE_MAX(RowsAtCompileTime,ColsAtCompileTime), EIGEN_SIZE_MAX(RowsAtCompileTime,ColsAtCompileTime)> MatrixBase< Derived >::SquareMatrixType

type of the equivalent square matrix

template<typename Derived>

typedef internal::stem_function<Scalar>::type MatrixBase< Derived >::StemFunction

template<typename Derived>

typedef MatrixBase MatrixBase< Derived >::StorageBaseType

template<typename Derived>

typedef internal::traits<Derived>::StorageKind MatrixBase< Derived >::StorageKind

Reimplemented from DenseBase< Derived >.

Member Enumeration Documentation

template<typename Derived>

anonymous enum

Enumerator:

SizeMinusOne

Constructor & Destructor Documentation

template<typename Derived>

MatrixBase< Derived >::MatrixBase ( ) [inline, protected]

Member Function Documentation

template<typename Derived >

const MatrixBase< Derived >::AdjointReturnType MatrixBase< Derived >::adjoint ( ) const [inline]

Returns:: an expression of the adjoint (i.e. conjugate transpose) of *this.

Example:

Output:

Warning:

If you want to replace a matrix by its own adjoint, do NOT do this:

 m = m.adjoint(); // bug!!! caused by aliasing effect

Instead, use the adjointInPlace() method:

 m.adjointInPlace();

which gives Eigen good opportunities for optimization, or alternatively you can also do:

 m = m.adjoint().eval();

See also:: adjointInPlace(), transpose(), conjugate(), class Transpose, class internal::scalar_conjugate_op

template<typename Derived >

void MatrixBase< Derived >::adjointInPlace ( ) [inline]

This is the "in place" version of adjoint(): it replaces *this by its own transpose. Thus, doing

 m.adjointInPlace();

has the same effect on m as doing

 m = m.adjoint().eval();

and is faster and also safer because in the latter line of code, forgetting the eval() results in a bug caused by aliasing.

Notice however that this method is only useful if you want to replace a matrix by its own adjoint. If you just need the adjoint of a matrix, use adjoint().

Note:: if the matrix is not square, then *this must be a resizable matrix.

See also:: transpose(), adjoint(), transposeInPlace()

template<typename Derived >

template<typename EssentialPart >

void MatrixBase< Derived >::applyHouseholderOnTheLeft	(	const EssentialPart &	essential,
		const Scalar &	tau,
		Scalar *	workspace
	)

template<typename Derived >

template<typename EssentialPart >

void MatrixBase< Derived >::applyHouseholderOnTheRight	(	const EssentialPart &	essential,
		const Scalar &	tau,
		Scalar *	workspace
	)

template<typename Derived >

template<typename OtherDerived >

void MatrixBase< Derived >::applyOnTheLeft ( const EigenBase< OtherDerived > & other ) [inline]

replaces *this by *this * other.

template<typename Derived >

template<typename OtherScalar >

void MatrixBase< Derived >::applyOnTheLeft	(	Index	p,
		Index	q,
		const JacobiRotation< OtherScalar > &	j
	)			`[inline]`

Applies the rotation in the plane j to the rows p and q of *this, i.e., it computes B = J * B, with 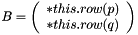$B = \left ( \begin{array}{cc} \text{*this.row}(p) \\ \text{*this.row}(q) \end{array} \right )$ .

See also:: class JacobiRotation, MatrixBase::applyOnTheRight(), internal::apply_rotation_in_the_plane()

template<typename Derived >

template<typename OtherDerived >

void MatrixBase< Derived >::applyOnTheRight ( const EigenBase< OtherDerived > & other ) [inline]

replaces *this by *this * other. It is equivalent to MatrixBase::operator*=()

template<typename Derived >

template<typename OtherScalar >

void MatrixBase< Derived >::applyOnTheRight	(	Index	p,
		Index	q,
		const JacobiRotation< OtherScalar > &	j
	)			`[inline]`

Applies the rotation in the plane j to the columns p and q of *this, i.e., it computes B = B * J with 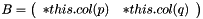$B = \left ( \begin{array}{cc} \text{*this.col}(p) & \text{*this.col}(q) \end{array} \right )$ .

See also:: class JacobiRotation, MatrixBase::applyOnTheLeft(), internal::apply_rotation_in_the_plane()

template<typename Derived>

ArrayWrapper<Derived> MatrixBase< Derived >::array ( ) [inline]

Returns:: an Array expression of this matrix

See also:: ArrayBase::matrix()

template<typename Derived>

const ArrayWrapper<Derived> MatrixBase< Derived >::array ( ) const [inline]

template<typename Derived >

const DiagonalWrapper< const Derived > MatrixBase< Derived >::asDiagonal ( ) const [inline]

Returns:: a pseudo-expression of a diagonal matrix with *this as vector of diagonal coefficients

Example:

Output:

See also:: class DiagonalWrapper, class DiagonalMatrix, diagonal(), isDiagonal()

template<typename Derived >

const PermutationWrapper< const Derived > MatrixBase< Derived >::asPermutation ( ) const

template<typename Derived>

template<typename CustomBinaryOp , typename OtherDerived >

EIGEN_STRONG_INLINE const CwiseBinaryOp<CustomBinaryOp, const Derived, const OtherDerived> MatrixBase< Derived >::binaryExpr	(	const EIGEN_CURRENT_STORAGE_BASE_CLASS< OtherDerived > &	other,
		const CustomBinaryOp &	func = `CustomBinaryOp()`
	)			const `[inline]`

Returns:: an expression of the difference of *this and other

Note:: If you want to substract a given scalar from all coefficients, see Cwise::operator-().

See also:: class CwiseBinaryOp, operator-=()

Returns:: an expression of the sum of *this and other

Note:: If you want to add a given scalar to all coefficients, see Cwise::operator+().

See also:: class CwiseBinaryOp, operator+=()

Returns:: an expression of a custom coefficient-wise operator func of *this and other

The template parameter CustomBinaryOp is the type of the functor of the custom operator (see class CwiseBinaryOp for an example)

Here is an example illustrating the use of custom functors:

Output:

See also:: class CwiseBinaryOp, operator+(), operator-(), cwiseProduct()

template<typename Derived >

NumTraits< typename internal::traits< Derived >::Scalar >::Real MatrixBase< Derived >::blueNorm ( ) const [inline]

Returns:: the l2 norm of *this using the Blue's algorithm. A Portable Fortran Program to Find the Euclidean Norm of a Vector, ACM TOMS, Vol 4, Issue 1, 1978.

For architecture/scalar types without vectorization, this version is much faster than stableNorm(). Otherwise the stableNorm() is faster.

See also:: norm(), stableNorm(), hypotNorm()

template<typename Derived>

template<typename NewType >

internal::cast_return_type<Derived,const CwiseUnaryOp<internal::scalar_cast_op<typename internal::traits<Derived>::Scalar, NewType>, const Derived> >::type MatrixBase< Derived >::cast ( ) const [inline]

Returns:: an expression of *this with the Scalar type casted to NewScalar.

The template parameter NewScalar is the type we are casting the scalars to.

See also:: class CwiseUnaryOp

template<typename Derived >

const ColPivHouseholderQR< typename MatrixBase< Derived >::PlainObject > MatrixBase< Derived >::colPivHouseholderQr ( ) const

Returns:: the column-pivoting Householder QR decomposition of *this.

See also:: class ColPivHouseholderQR

template<typename Derived >

template<typename ResultType >

void MatrixBase< Derived >::computeInverseAndDetWithCheck	(	ResultType &	inverse,
		typename ResultType::Scalar &	determinant,
		bool &	invertible,
		const RealScalar &	absDeterminantThreshold = `NumTraits<Scalar>::dummy_precision()`
	)			const `[inline]`

Computation of matrix inverse and determinant, with invertibility check.

This is only for fixed-size square matrices of size up to 4x4.

Parameters:

	inverse	Reference to the matrix in which to store the inverse.
	determinant	Reference to the variable in which to store the inverse.
	invertible	Reference to the bool variable in which to store whether the matrix is invertible.
	absDeterminantThreshold	Optional parameter controlling the invertibility check. The matrix will be declared invertible if the absolute value of its determinant is greater than this threshold.

Example:

Output:

See also:: inverse(), computeInverseWithCheck()

template<typename Derived >

template<typename ResultType >

void MatrixBase< Derived >::computeInverseWithCheck	(	ResultType &	inverse,
		bool &	invertible,
		const RealScalar &	absDeterminantThreshold = `NumTraits<Scalar>::dummy_precision()`
	)			const `[inline]`

Computation of matrix inverse, with invertibility check.

This is only for fixed-size square matrices of size up to 4x4.

Parameters:

	inverse	Reference to the matrix in which to store the inverse.
	invertible	Reference to the bool variable in which to store whether the matrix is invertible.
	absDeterminantThreshold	Optional parameter controlling the invertibility check. The matrix will be declared invertible if the absolute value of its determinant is greater than this threshold.

Example:

Output:

See also:: inverse(), computeInverseAndDetWithCheck()

template<typename Derived>

ConjugateReturnType MatrixBase< Derived >::conjugate ( ) const [inline]

Returns:: an expression of the complex conjugate of *this.

See also:: adjoint()

template<typename Derived>

const MatrixFunctionReturnValue<Derived> MatrixBase< Derived >::cos ( ) const

template<typename Derived>

const MatrixFunctionReturnValue<Derived> MatrixBase< Derived >::cosh ( ) const

template<typename Derived >

template<typename OtherDerived >

MatrixBase< Derived >::template cross_product_return_type< OtherDerived >::type MatrixBase< Derived >::cross ( const MatrixBase< OtherDerived > & other ) const [inline]

Returns:: the cross product of *this and other

Here is a very good explanation of cross-product: http://xkcd.com/199/

See also:: MatrixBase::cross3()

template<typename Derived >

template<typename OtherDerived >

MatrixBase< Derived >::PlainObject MatrixBase< Derived >::cross3 ( const MatrixBase< OtherDerived > & other ) const [inline]

Returns:: the cross product of *this and other using only the x, y, and z coefficients

The size of *this and other must be four. This function is especially useful when using 4D vectors instead of 3D ones to get advantage of SSE/AltiVec vectorization.

See also:: MatrixBase::cross()

template<typename Derived>

EIGEN_STRONG_INLINE const CwiseUnaryOp<internal::scalar_abs_op<Scalar>, const Derived> MatrixBase< Derived >::cwiseAbs ( ) const [inline]

Returns:: an expression of the coefficient-wise absolute value of *this

Example:

Output:

See also:: cwiseAbs2()

template<typename Derived>

EIGEN_STRONG_INLINE const CwiseUnaryOp<internal::scalar_abs2_op<Scalar>, const Derived> MatrixBase< Derived >::cwiseAbs2 ( ) const [inline]

Returns:: an expression of the coefficient-wise squared absolute value of *this

Example:

Output:

See also:: cwiseAbs()

template<typename Derived>

const CwiseUnaryOp<std::binder1st<std::equal_to<Scalar> >, const Derived> MatrixBase< Derived >::cwiseEqual ( const Scalar & s ) const [inline]

Returns:: an expression of the coefficient-wise == operator of *this and a scalar s

Warning:: this performs an exact comparison, which is generally a bad idea with floating-point types. In order to check for equality between two vectors or matrices with floating-point coefficients, it is generally a far better idea to use a fuzzy comparison as provided by isApprox() and isMuchSmallerThan().

See also:: cwiseEqual(const MatrixBase<OtherDerived> &) const

template<typename Derived>

template<typename OtherDerived >

const CwiseBinaryOp<std::equal_to<Scalar>, const Derived, const OtherDerived> MatrixBase< Derived >::cwiseEqual ( const EIGEN_CURRENT_STORAGE_BASE_CLASS< OtherDerived > & other ) const [inline]

Returns:: an expression of the coefficient-wise == operator of *this and other

Warning:: this performs an exact comparison, which is generally a bad idea with floating-point types. In order to check for equality between two vectors or matrices with floating-point coefficients, it is generally a far better idea to use a fuzzy comparison as provided by isApprox() and isMuchSmallerThan().

Example:

Output:

See also:: cwiseNotEqual(), isApprox(), isMuchSmallerThan()

template<typename Derived>

const CwiseUnaryOp<internal::scalar_inverse_op<Scalar>, const Derived> MatrixBase< Derived >::cwiseInverse ( ) const [inline]

Returns:: an expression of the coefficient-wise inverse of *this.

Example:

Output:

See also:: cwiseProduct()

template<typename Derived>

template<typename OtherDerived >

EIGEN_STRONG_INLINE const CwiseBinaryOp<internal::scalar_max_op<Scalar>, const Derived, const OtherDerived> MatrixBase< Derived >::cwiseMax ( const EIGEN_CURRENT_STORAGE_BASE_CLASS< OtherDerived > & other ) const [inline]

Returns:: an expression of the coefficient-wise max of *this and other

Example:

Output:

See also:: class CwiseBinaryOp, min()

template<typename Derived>

template<typename OtherDerived >

EIGEN_STRONG_INLINE const CwiseBinaryOp<internal::scalar_min_op<Scalar>, const Derived, const OtherDerived> MatrixBase< Derived >::cwiseMin ( const EIGEN_CURRENT_STORAGE_BASE_CLASS< OtherDerived > & other ) const [inline]

Returns:: an expression of the coefficient-wise min of *this and other

Example:

Output:

See also:: class CwiseBinaryOp, max()

template<typename Derived>

template<typename OtherDerived >

const CwiseBinaryOp<std::not_equal_to<Scalar>, const Derived, const OtherDerived> MatrixBase< Derived >::cwiseNotEqual ( const EIGEN_CURRENT_STORAGE_BASE_CLASS< OtherDerived > & other ) const [inline]

Returns:: an expression of the coefficient-wise != operator of *this and other

Warning:: this performs an exact comparison, which is generally a bad idea with floating-point types. In order to check for equality between two vectors or matrices with floating-point coefficients, it is generally a far better idea to use a fuzzy comparison as provided by isApprox() and isMuchSmallerThan().

Example:

Output:

See also:: cwiseEqual(), isApprox(), isMuchSmallerThan()

template<typename Derived>

template<typename OtherDerived >

EIGEN_STRONG_INLINE const CwiseBinaryOp<internal::scalar_quotient_op<Scalar>, const Derived, const OtherDerived> MatrixBase< Derived >::cwiseQuotient ( const EIGEN_CURRENT_STORAGE_BASE_CLASS< OtherDerived > & other ) const [inline]

Returns:: an expression of the coefficient-wise quotient of *this and other

Example:

Output:

See also:: class CwiseBinaryOp, cwiseProduct(), cwiseInverse()

template<typename Derived>

const CwiseUnaryOp<internal::scalar_sqrt_op<Scalar>, const Derived> MatrixBase< Derived >::cwiseSqrt ( ) const [inline]

Returns:: an expression of the coefficient-wise square root of *this.

Example:

Output:

See also:: cwisePow(), cwiseSquare()

template<typename Derived >

internal::traits< Derived >::Scalar MatrixBase< Derived >::determinant ( ) const [inline]

Returns:: the determinant of this matrix

template<typename Derived >

MatrixBase< Derived >::template DiagonalIndexReturnType< Index >::Type MatrixBase< Derived >::diagonal ( ) [inline]

Returns:: an expression of the main diagonal of the matrix *this

*this is not required to be square.

Example:

Output:

See also:: class Diagonal

Returns:: an expression of the DiagIndex-th sub or super diagonal of the matrix *this

*this is not required to be square.

The template parameter DiagIndex represent a super diagonal if DiagIndex > 0 and a sub diagonal otherwise. DiagIndex == 0 is equivalent to the main diagonal.

Example:

Output:

See also:: MatrixBase::diagonal(), class Diagonal

template<typename Derived >

MatrixBase< Derived >::template ConstDiagonalIndexReturnType< Index >::Type MatrixBase< Derived >::diagonal ( ) const [inline]

This is the const version of diagonal().

This is the const version of diagonal<int>().

template<typename Derived>

template<int Index>

DiagonalIndexReturnType<Index>::Type MatrixBase< Derived >::diagonal ( )

template<typename Derived >

MatrixBase< Derived >::template DiagonalIndexReturnType< Dynamic >::Type MatrixBase< Derived >::diagonal ( Index index ) [inline]

Returns:: an expression of the DiagIndex-th sub or super diagonal of the matrix *this

*this is not required to be square.

The template parameter DiagIndex represent a super diagonal if DiagIndex > 0 and a sub diagonal otherwise. DiagIndex == 0 is equivalent to the main diagonal.

Example:

Output:

See also:: MatrixBase::diagonal(), class Diagonal

template<typename Derived>

template<int Index>

ConstDiagonalIndexReturnType<Index>::Type MatrixBase< Derived >::diagonal ( ) const

template<typename Derived >

MatrixBase< Derived >::template ConstDiagonalIndexReturnType< Dynamic >::Type MatrixBase< Derived >::diagonal ( Index index ) const [inline]

This is the const version of diagonal(Index).

template<typename Derived>

Index MatrixBase< Derived >::diagonalSize ( ) const [inline]

Returns:: the size of the main diagonal, which is min(rows(),cols()).

See also:: rows(), cols(), SizeAtCompileTime.

template<typename Derived >

template<typename OtherDerived >

internal::scalar_product_traits< typename internal::traits< Derived >::Scalar, typename internal::traits< OtherDerived >::Scalar >::ReturnType MatrixBase< Derived >::dot ( const MatrixBase< OtherDerived > & other ) const

Returns:: the dot product of *this with other.

Note:: If the scalar type is complex numbers, then this function returns the hermitian (sesquilinear) dot product, conjugate-linear in the first variable and linear in the second variable.

See also:: squaredNorm(), norm()

template<typename Derived>

template<typename OtherDerived >

EIGEN_STRONG_INLINE const MatrixBase< Derived >::EIGEN_CWISE_PRODUCT_RETURN_TYPE	(	Derived	,
		OtherDerived
	)			const `[inline]`

Returns:: an expression of the Schur product (coefficient wise product) of *this and other

Example:

Output:

See also:: class CwiseBinaryOp, cwiseAbs2

template<typename Derived >

MatrixBase< Derived >::EigenvaluesReturnType MatrixBase< Derived >::eigenvalues ( ) const [inline]

Computes the eigenvalues of a matrix.

Returns:: Column vector containing the eigenvalues.

This function computes the eigenvalues with the help of the EigenSolver class (for real matrices) or the ComplexEigenSolver class (for complex matrices).

The eigenvalues are repeated according to their algebraic multiplicity, so there are as many eigenvalues as rows in the matrix.

The SelfAdjointView class provides a better algorithm for selfadjoint matrices.

Example:

Output:

See also:: EigenSolver::eigenvalues(), ComplexEigenSolver::eigenvalues(), SelfAdjointView::eigenvalues()

template<typename Derived>

const MatrixExponentialReturnValue<Derived> MatrixBase< Derived >::exp ( ) const

template<typename Derived >

const ForceAlignedAccess< Derived > MatrixBase< Derived >::forceAlignedAccess ( ) const [inline]

Returns:: an expression of *this with forced aligned access

See also:: forceAlignedAccessIf(),class ForceAlignedAccess

Reimplemented from DenseBase< Derived >.

template<typename Derived >

ForceAlignedAccess< Derived > MatrixBase< Derived >::forceAlignedAccess ( ) [inline]

Returns:: an expression of *this with forced aligned access

See also:: forceAlignedAccessIf(), class ForceAlignedAccess

Reimplemented from DenseBase< Derived >.

template<typename Derived >

template<bool Enable>

internal::add_const_on_value_type< typename internal::conditional< Enable, ForceAlignedAccess< Derived >, Derived & >::type >::type MatrixBase< Derived >::forceAlignedAccessIf ( ) const [inline]

Returns:: an expression of *this with forced aligned access if Enable is true.

See also:: forceAlignedAccess(), class ForceAlignedAccess

Reimplemented from DenseBase< Derived >.

template<typename Derived >

template<bool Enable>

internal::conditional< Enable, ForceAlignedAccess< Derived >, Derived & >::type MatrixBase< Derived >::forceAlignedAccessIf ( ) [inline]

Returns:: an expression of *this with forced aligned access if Enable is true.

See also:: forceAlignedAccess(), class ForceAlignedAccess

Reimplemented from DenseBase< Derived >.

template<typename Derived >

const FullPivHouseholderQR< typename MatrixBase< Derived >::PlainObject > MatrixBase< Derived >::fullPivHouseholderQr ( ) const

Returns:: the full-pivoting Householder QR decomposition of *this.

See also:: class FullPivHouseholderQR

template<typename Derived >

const FullPivLU< typename MatrixBase< Derived >::PlainObject > MatrixBase< Derived >::fullPivLu ( ) const [inline]

Returns:: the full-pivoting LU decomposition of *this.

See also:: class FullPivLU

template<typename Derived >

const MatrixBase< Derived >::HNormalizedReturnType MatrixBase< Derived >::hnormalized ( ) const [inline]

Returns:: an expression of the homogeneous normalized vector of *this

Example:

Output:

See also:: VectorwiseOp::hnormalized()

template<typename Derived >

const HouseholderQR< typename MatrixBase< Derived >::PlainObject > MatrixBase< Derived >::householderQr ( ) const

Returns:: the Householder QR decomposition of *this.

See also:: class HouseholderQR

template<typename Derived >

NumTraits< typename internal::traits< Derived >::Scalar >::Real MatrixBase< Derived >::hypotNorm ( ) const [inline]

Returns:: the l2 norm of *this avoiding undeflow and overflow. This version use a concatenation of hypot() calls, and it is very slow.

See also:: norm(), stableNorm()

template<typename Derived >

EIGEN_STRONG_INLINE const MatrixBase< Derived >::IdentityReturnType MatrixBase< Derived >::Identity ( ) [static]

Returns:: an expression of the identity matrix (not necessarily square).

This variant is only for fixed-size MatrixBase types. For dynamic-size types, you need to use the variant taking size arguments.

Example:

Output:

See also:: Identity(Index,Index), setIdentity(), isIdentity()

template<typename Derived >

EIGEN_STRONG_INLINE const MatrixBase< Derived >::IdentityReturnType MatrixBase< Derived >::Identity	(	Index	rows,
		Index	cols
	)			`[static]`

Returns:: an expression of the identity matrix (not necessarily square).

The parameters rows and cols are the number of rows and of columns of the returned matrix. Must be compatible with this MatrixBase type.

This variant is meant to be used for dynamic-size matrix types. For fixed-size types, it is redundant to pass rows and cols as arguments, so Identity() should be used instead.

Example:

Output:

See also:: Identity(), setIdentity(), isIdentity()

template<typename Derived>

const ImagReturnType MatrixBase< Derived >::imag ( ) const [inline]

Returns:: an read-only expression of the imaginary part of *this.

See also:: real()

template<typename Derived>

NonConstImagReturnType MatrixBase< Derived >::imag ( ) [inline]

Returns:: a non const expression of the imaginary part of *this.

See also:: real()

template<typename Derived >

const internal::inverse_impl< Derived > MatrixBase< Derived >::inverse ( ) const [inline]

Returns:: the matrix inverse of this matrix.

For small fixed sizes up to 4x4, this method uses cofactors. In the general case, this method uses class PartialPivLU.

Note:

This matrix must be invertible, otherwise the result is undefined. If you need an invertibility check, do the following:

for fixed sizes up to 4x4, use computeInverseAndDetWithCheck().
for the general case, use class FullPivLU.

Example:

Output:

See also:: computeInverseAndDetWithCheck()

template<typename Derived >

bool MatrixBase< Derived >::isDiagonal ( RealScalar prec = NumTraits<Scalar>::dummy_precision() ) const

Returns:: true if *this is approximately equal to a diagonal matrix, within the precision given by prec.

Example:

Output:

See also:: asDiagonal()

template<typename Derived >

bool MatrixBase< Derived >::isIdentity ( RealScalar prec = NumTraits<Scalar>::dummy_precision() ) const

Returns:: true if *this is approximately equal to the identity matrix (not necessarily square), within the precision given by prec.

Example:

Output:

See also:: class CwiseNullaryOp, Identity(), Identity(Index,Index), setIdentity()

template<typename Derived >

bool MatrixBase< Derived >::isLowerTriangular ( RealScalar prec = NumTraits<Scalar>::dummy_precision() ) const

Returns:: true if *this is approximately equal to a lower triangular matrix, within the precision given by prec.

See also:: isUpperTriangular()

template<typename Derived >

template<typename OtherDerived >

bool MatrixBase< Derived >::isOrthogonal	(	const MatrixBase< OtherDerived > &	other,
		RealScalar	prec = `NumTraits<Scalar>::dummy_precision()`
	)			const

Returns:: true if *this is approximately orthogonal to other, within the precision given by prec.

Example:

Output:

template<typename Derived >

bool MatrixBase< Derived >::isUnitary ( RealScalar prec = NumTraits<Scalar>::dummy_precision() ) const

Returns:: true if *this is approximately an unitary matrix, within the precision given by prec. In the case where the Scalar type is real numbers, a unitary matrix is an orthogonal matrix, whence the name.

Note:: This can be used to check whether a family of vectors forms an orthonormal basis. Indeed, m.isUnitary() returns true if and only if the columns (equivalently, the rows) of m form an orthonormal basis.

Example:

Output:

template<typename Derived >

bool MatrixBase< Derived >::isUpperTriangular ( RealScalar prec = NumTraits<Scalar>::dummy_precision() ) const

Returns:: true if *this is approximately equal to an upper triangular matrix, within the precision given by prec.

See also:: isLowerTriangular()

template<typename Derived >

JacobiSVD< typename MatrixBase< Derived >::PlainObject > MatrixBase< Derived >::jacobiSvd ( unsigned int computationOptions = 0 ) const

template<typename Derived >

template<typename ProductDerived , typename Lhs , typename Rhs >

Derived & MatrixBase< Derived >::lazyAssign ( const ProductBase< ProductDerived, Lhs, Rhs > & other )

template<typename Derived >

template<typename OtherDerived >

const LazyProductReturnType< Derived, OtherDerived >::Type MatrixBase< Derived >::lazyProduct ( const MatrixBase< OtherDerived > & other ) const

Returns:: an expression of the matrix product of *this and other without implicit evaluation.

The returned product will behave like any other expressions: the coefficients of the product will be computed once at a time as requested. This might be useful in some extremely rare cases when only a small and no coherent fraction of the result's coefficients have to be computed.

Warning:: This version of the matrix product can be much much slower. So use it only if you know what you are doing and that you measured a true speed improvement.

See also:: operator*(const MatrixBase&)

template<typename Derived >

const LDLT< typename MatrixBase< Derived >::PlainObject > MatrixBase< Derived >::ldlt ( ) const [inline]

Returns:: the Cholesky decomposition with full pivoting without square root of *this

template<typename Derived >

const LLT< typename MatrixBase< Derived >::PlainObject > MatrixBase< Derived >::llt ( ) const [inline]

Returns:: the LLT decomposition of *this

template<typename Derived >

template<int p>

NumTraits< typename internal::traits< Derived >::Scalar >::Real MatrixBase< Derived >::lpNorm ( ) const [inline]

Returns:: the 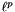$\ell^p$ norm of *this, that is, returns the p-th root of the sum of the p-th powers of the absolute values of the coefficients of *this. If p is the special value Eigen::Infinity, this function returns the 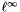$\ell^\infty$ norm, that is the maximum of the absolute values of the coefficients of *this.

See also:: norm()

Reimplemented from DenseBase< Derived >.

template<typename Derived >

template<typename EssentialPart >

void MatrixBase< Derived >::makeHouseholder	(	EssentialPart &	essential,
		Scalar &	tau,
		RealScalar &	beta
	)			const

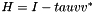Computes the elementary reflector H such that: $ H *this = [ beta 0 ... 0]^T $ where the transformation H is: $ H = I - tau v v^*$ and the vector v is: $ v^T = [1 essential^T] $

On output:

Parameters:

	essential	the essential part of the vector `v`
	tau	the scaling factor of the householder transformation
	beta	the result of H * `*this`

See also:: MatrixBase::makeHouseholderInPlace(), MatrixBase::applyHouseholderOnTheLeft(), MatrixBase::applyHouseholderOnTheRight()

template<typename Derived >

void MatrixBase< Derived >::makeHouseholderInPlace	(	Scalar &	tau,
		RealScalar &	beta
	)

template<typename Derived>

MatrixBase<Derived>& MatrixBase< Derived >::matrix ( ) [inline]

template<typename Derived>

const MatrixBase<Derived>& MatrixBase< Derived >::matrix ( ) const [inline]

template<typename Derived>

const MatrixFunctionReturnValue<Derived> MatrixBase< Derived >::matrixFunction ( StemFunction f ) const

template<typename Derived >

NoAlias< Derived, MatrixBase > MatrixBase< Derived >::noalias ( )

Returns:: a pseudo expression of *this with an operator= assuming no aliasing between *this and the source expression.

More precisely, noalias() allows to bypass the EvalBeforeAssignBit flag. Currently, even though several expressions may alias, only product expressions have this flag. Therefore, noalias() is only usefull when the source expression contains a matrix product.

Here are some examples where noalias is usefull:

 D.noalias()  = A * B;
 D.noalias() += A.transpose() * B;
 D.noalias() -= 2 * A * B.adjoint();

On the other hand the following example will lead to a wrong result:

 A.noalias() = A * B;

because the result matrix A is also an operand of the matrix product. Therefore, there is no alternative than evaluating A * B in a temporary, that is the default behavior when you write:

 A = A * B;

See also:: class NoAlias

template<typename Derived >

NumTraits< typename internal::traits< Derived >::Scalar >::Real MatrixBase< Derived >::norm ( ) const [inline]

Returns:: the l2 norm of *this, i.e., for vectors, the square root of the dot product of *this with itself.

See also:: dot(), squaredNorm()

template<typename Derived >

void MatrixBase< Derived >::normalize ( ) [inline]

Normalizes the vector, i.e. divides it by its own norm.

See also:: norm(), normalized()

template<typename Derived >

const MatrixBase< Derived >::PlainObject MatrixBase< Derived >::normalized ( ) const [inline]

Returns:: an expression of the quotient of *this by its own norm.

See also:: norm(), normalize()

template<typename Derived>

template<typename OtherDerived >

bool MatrixBase< Derived >::operator!= ( const MatrixBase< OtherDerived > & other ) const [inline]

Returns:: true if at least one pair of coefficients of *this and other are not exactly equal to each other.

Warning:: When using floating point scalar values you probably should rather use a fuzzy comparison such as isApprox()

See also:: isApprox(), operator==

template<typename Derived >

template<typename OtherDerived >

const ProductReturnType< Derived, OtherDerived >::Type MatrixBase< Derived >::operator* ( const MatrixBase< OtherDerived > & other ) const [inline]

Returns:: the matrix product of *this and other.

Note:: If instead of the matrix product you want the coefficient-wise product, see Cwise::operator*().

See also:: lazyProduct(), operator*=(const MatrixBase&), Cwise::operator*()

template<typename Derived>

const CwiseUnaryOp<internal::scalar_multiple2_op<Scalar,std::complex<Scalar> >, const Derived> MatrixBase< Derived >::operator* ( const std::complex< Scalar > & scalar ) const [inline]

Overloaded for efficient real matrix times complex scalar value

template<typename Derived >

template<typename DiagonalDerived >

const DiagonalProduct< Derived, DiagonalDerived, OnTheRight > MatrixBase< Derived >::operator* ( const DiagonalBase< DiagonalDerived > & diagonal ) const [inline]

Returns:: the diagonal matrix product of *this by the diagonal matrix diagonal.

template<typename Derived>

const ScalarMultipleReturnType MatrixBase< Derived >::operator* ( const Scalar & scalar ) const [inline]

Returns:: an expression of *this scaled by the scalar factor scalar

template<typename Derived>

template<typename Derived >

MatrixBase<Derived>::ScalarMultipleReturnType MatrixBase< Derived >::operator* ( const UniformScaling< Scalar > & s ) const

Concatenates a linear transformation matrix and a uniform scaling

template<typename Derived >

template<typename OtherDerived >

Derived & MatrixBase< Derived >::operator*= ( const EigenBase< OtherDerived > & other ) [inline]

replaces *this by *this * other.

Returns:: a reference to *this

template<typename Derived >

template<typename OtherDerived >

EIGEN_STRONG_INLINE Derived & MatrixBase< Derived >::operator+= ( const MatrixBase< OtherDerived > & other )

replaces *this by *this + other.

Returns:: a reference to *this

template<typename Derived>

template<typename OtherDerived >

Derived& MatrixBase< Derived >::operator+= ( const ArrayBase< OtherDerived > & ) [inline, protected]

template<typename Derived>

const CwiseUnaryOp<internal::scalar_opposite_op<typename internal::traits<Derived>::Scalar>, const Derived> MatrixBase< Derived >::operator- ( ) const [inline]

Returns:: an expression of the opposite of *this

template<typename Derived >

template<typename OtherDerived >

EIGEN_STRONG_INLINE Derived & MatrixBase< Derived >::operator-= ( const MatrixBase< OtherDerived > & other )

replaces *this by *this - other.

Returns:: a reference to *this

template<typename Derived>

template<typename OtherDerived >

Derived& MatrixBase< Derived >::operator-= ( const ArrayBase< OtherDerived > & ) [inline, protected]

template<typename Derived>

const CwiseUnaryOp<internal::scalar_quotient1_op<typename internal::traits<Derived>::Scalar>, const Derived> MatrixBase< Derived >::operator/ ( const Scalar & scalar ) const [inline]

Returns:: an expression of *this divided by the scalar value scalar

template<typename Derived >

template<typename OtherDerived >

EIGEN_STRONG_INLINE Derived & MatrixBase< Derived >::operator= ( const DenseBase< OtherDerived > & other )

Copies other into *this.

Returns:: a reference to *this.

Reimplemented from DenseBase< Derived >.

template<typename Derived >

template<typename OtherDerived >

EIGEN_STRONG_INLINE Derived & MatrixBase< Derived >::operator= ( const ReturnByValue< OtherDerived > & other )

Reimplemented from DenseBase< Derived >.

template<typename Derived >

template<typename OtherDerived >

EIGEN_STRONG_INLINE Derived & MatrixBase< Derived >::operator= ( const EigenBase< OtherDerived > & other )

Copies the generic expression other into *this.

The expression must provide a (templated) evalTo(Derived& dst) const function which does the actual job. In practice, this allows any user to write its own special matrix without having to modify MatrixBase

Returns:: a reference to *this.

Reimplemented from DenseBase< Derived >.

template<typename Derived >

EIGEN_STRONG_INLINE Derived & MatrixBase< Derived >::operator= ( const MatrixBase< Derived > & other )

Special case of the template operator=, in order to prevent the compiler from generating a default operator= (issue hit with g++ 4.1)

template<typename Derived>

template<typename OtherDerived >

bool MatrixBase< Derived >::operator== ( const MatrixBase< OtherDerived > & other ) const [inline]

Returns:: true if each coefficients of *this and other are all exactly equal.

Warning:: When using floating point scalar values you probably should rather use a fuzzy comparison such as isApprox()

See also:: isApprox(), operator!=

template<typename Derived >

MatrixBase< Derived >::RealScalar MatrixBase< Derived >::operatorNorm ( ) const [inline]

Computes the L2 operator norm.

Returns:: Operator norm of the matrix.

This function computes the L2 operator norm of a matrix, which is also known as the spectral norm. The norm of a matrix 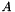$ A $ is defined to be

$\|A\|_2 = \max_x \frac{\|Ax\|_2}{\|x\|_2}$

where the maximum is over all vectors and the norm on the right is the Euclidean vector norm. The norm equals the largest singular value, which is the square root of the largest eigenvalue of the positive semi-definite matrix 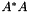$ A^*A $ .

The current implementation uses the eigenvalues of 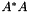$ A^*A $ , as computed by SelfAdjointView::eigenvalues(), to compute the operator norm of a matrix. The SelfAdjointView class provides a better algorithm for selfadjoint matrices.

Example:

Output:

See also:: SelfAdjointView::eigenvalues(), SelfAdjointView::operatorNorm()

template<typename Derived >

const PartialPivLU< typename MatrixBase< Derived >::PlainObject > MatrixBase< Derived >::partialPivLu ( ) const [inline]

Returns:: the partial-pivoting LU decomposition of *this.

See also:: class PartialPivLU

template<typename Derived>

NonConstRealReturnType MatrixBase< Derived >::real ( ) [inline]

Returns:: a non const expression of the real part of *this.

See also:: imag()

template<typename Derived>

RealReturnType MatrixBase< Derived >::real ( ) const [inline]

Returns:: a read-only expression of the real part of *this.

See also:: imag()

template<typename Derived >

template<unsigned int UpLo>

MatrixBase< Derived >::template ConstSelfAdjointViewReturnType< UpLo >::Type MatrixBase< Derived >::selfadjointView ( ) const

template<typename Derived >

template<unsigned int UpLo>

MatrixBase< Derived >::template SelfAdjointViewReturnType< UpLo >::Type MatrixBase< Derived >::selfadjointView ( )

template<typename Derived >

EIGEN_STRONG_INLINE Derived & MatrixBase< Derived >::setIdentity	(	Index	rows,
		Index	cols
	)

Resizes to the given size, and writes the identity expression (not necessarily square) into *this.

Parameters:

	rows	the new number of rows
	cols	the new number of columns

Example:

Output:

See also:: MatrixBase::setIdentity(), class CwiseNullaryOp, MatrixBase::Identity()

template<typename Derived >

EIGEN_STRONG_INLINE Derived & MatrixBase< Derived >::setIdentity ( )

Writes the identity expression (not necessarily square) into *this.

Example:

Output:

See also:: class CwiseNullaryOp, Identity(), Identity(Index,Index), isIdentity()

template<typename Derived>

const MatrixFunctionReturnValue<Derived> MatrixBase< Derived >::sin ( ) const

template<typename Derived>

const MatrixFunctionReturnValue<Derived> MatrixBase< Derived >::sinh ( ) const

template<typename Derived >

const SparseView< Derived > MatrixBase< Derived >::sparseView	(	const Scalar &	m_reference = `Scalar(0)`,
		typename NumTraits< Scalar >::Real	m_epsilon = `NumTraits<Scalar>::dummy_precision()`
	)			const

template<typename Derived >

EIGEN_STRONG_INLINE NumTraits< typename internal::traits< Derived >::Scalar >::Real MatrixBase< Derived >::squaredNorm ( ) const

Returns:: the squared l2 norm of *this, i.e., for vectors, the dot product of *this with itself.

See also:: dot(), norm()

template<typename Derived >

NumTraits< typename internal::traits< Derived >::Scalar >::Real MatrixBase< Derived >::stableNorm ( ) const [inline]

Returns:: the l2 norm of *this avoiding underflow and overflow. This version use a blockwise two passes algorithm: 1 - find the absolute largest coefficient s 2 - compute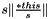 $s \Vert \frac{*this}{s} \Vert$ in a standard way

For architecture/scalar types supporting vectorization, this version is faster than blueNorm(). Otherwise the blueNorm() is much faster.

See also:: norm(), blueNorm(), hypotNorm()

template<typename Derived >

EIGEN_STRONG_INLINE internal::traits< Derived >::Scalar MatrixBase< Derived >::trace ( ) const

Returns:: the trace of *this, i.e. the sum of the coefficients on the main diagonal.

*this can be any matrix, not necessarily square.

See also:: diagonal(), sum()

Reimplemented from DenseBase< Derived >.

template<typename Derived >

template<unsigned int Mode>

MatrixBase< Derived >::template ConstTriangularViewReturnType< Mode >::Type MatrixBase< Derived >::triangularView ( ) const

This is the const version of MatrixBase::triangularView()

template<typename Derived >

template<unsigned int Mode>

MatrixBase< Derived >::template TriangularViewReturnType< Mode >::Type MatrixBase< Derived >::triangularView ( )

Returns:: an expression of a triangular view extracted from the current matrix

The parameter Mode can have the following values: Upper, StrictlyUpper, UnitUpper, Lower, StrictlyLower, UnitLower.

Example:

Output:

See also:: class TriangularView

template<typename Derived>

template<typename CustomUnaryOp >

const CwiseUnaryOp<CustomUnaryOp, const Derived> MatrixBase< Derived >::unaryExpr ( const CustomUnaryOp & func = CustomUnaryOp() ) const [inline]

Apply a unary operator coefficient-wise.

Parameters:

[in] func Functor implementing the unary operator

Template Parameters:

CustomUnaryOp

Type of func

Returns:: An expression of a custom coefficient-wise unary operator func of *this

The function ptr_fun() from the C++ standard library can be used to make functors out of normal functions.

Example:

Output:

Genuine functors allow for more possibilities, for instance it may contain a state.

Example:

Output:

See also:: class CwiseUnaryOp, class CwiseBinaryOp

template<typename Derived>

template<typename CustomViewOp >

const CwiseUnaryView<CustomViewOp, const Derived> MatrixBase< Derived >::unaryViewExpr ( const CustomViewOp & func = CustomViewOp() ) const [inline]

Returns:: an expression of a custom coefficient-wise unary operator func of *this

The template parameter CustomUnaryOp is the type of the functor of the custom unary operator.

Example:

Output:

See also:: class CwiseUnaryOp, class CwiseBinaryOp

template<typename Derived >

EIGEN_STRONG_INLINE const MatrixBase< Derived >::BasisReturnType MatrixBase< Derived >::Unit ( Index i ) [static]

Returns:: an expression of the i-th unit (basis) vector.

This variant is for fixed-size vector only.

See also:: MatrixBase::Unit(Index,Index), MatrixBase::UnitX(), MatrixBase::UnitY(), MatrixBase::UnitZ(), MatrixBase::UnitW()

template<typename Derived >

EIGEN_STRONG_INLINE const MatrixBase< Derived >::BasisReturnType MatrixBase< Derived >::Unit	(	Index	size,
		Index	i
	)			`[static]`

Returns:: an expression of the i-th unit (basis) vector.

See also:: MatrixBase::Unit(Index), MatrixBase::UnitX(), MatrixBase::UnitY(), MatrixBase::UnitZ(), MatrixBase::UnitW()

template<typename Derived >

MatrixBase< Derived >::PlainObject MatrixBase< Derived >::unitOrthogonal ( void ) const

Returns:: a unit vector which is orthogonal to *this

The size of *this must be at least 2. If the size is exactly 2, then the returned vector is a counter clock wise rotation of *this, i.e., (-y,x).normalized().

See also:: cross()

template<typename Derived >

EIGEN_STRONG_INLINE const MatrixBase< Derived >::BasisReturnType MatrixBase< Derived >::UnitW ( ) [static]

Returns:: an expression of the W axis unit vector (0,0,0,1)

See also:: MatrixBase::Unit(Index,Index), MatrixBase::Unit(Index), MatrixBase::UnitY(), MatrixBase::UnitZ(), MatrixBase::UnitW()

template<typename Derived >

EIGEN_STRONG_INLINE const MatrixBase< Derived >::BasisReturnType MatrixBase< Derived >::UnitX ( ) [static]

Returns:: an expression of the X axis unit vector (1{,0}^*)

See also:: MatrixBase::Unit(Index,Index), MatrixBase::Unit(Index), MatrixBase::UnitY(), MatrixBase::UnitZ(), MatrixBase::UnitW()

template<typename Derived >

EIGEN_STRONG_INLINE const MatrixBase< Derived >::BasisReturnType MatrixBase< Derived >::UnitY ( ) [static]

Returns:: an expression of the Y axis unit vector (0,1{,0}^*)

See also:: MatrixBase::Unit(Index,Index), MatrixBase::Unit(Index), MatrixBase::UnitY(), MatrixBase::UnitZ(), MatrixBase::UnitW()

template<typename Derived >

EIGEN_STRONG_INLINE const MatrixBase< Derived >::BasisReturnType MatrixBase< Derived >::UnitZ ( ) [static]

Returns:: an expression of the Z axis unit vector (0,0,1{,0}^*)

See also:: MatrixBase::Unit(Index,Index), MatrixBase::Unit(Index), MatrixBase::UnitY(), MatrixBase::UnitZ(), MatrixBase::UnitW()

Friends And Related Function Documentation

template<typename Derived>

const ScalarMultipleReturnType operator*	(	const Scalar &	scalar,
		const StorageBaseType &	matrix
	)			`[friend]`

template<typename Derived>

const CwiseUnaryOp<internal::scalar_multiple2_op<Scalar,std::complex<Scalar> >, const Derived> operator*	(	const std::complex< Scalar > &	scalar,
		const StorageBaseType &	matrix
	)			`[friend]`

The documentation for this class was generated from the following files:

/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Core/MatrixBase.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/plugins/CommonCwiseUnaryOps.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/plugins/CommonCwiseBinaryOps.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/plugins/MatrixCwiseUnaryOps.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/plugins/MatrixCwiseBinaryOps.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Cholesky/LDLT.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Cholesky/LLT.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Core/Assign.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Core/CwiseBinaryOp.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Core/CwiseNullaryOp.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Core/Diagonal.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Core/DiagonalMatrix.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Core/DiagonalProduct.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Core/Dot.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Core/EigenBase.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Core/ForceAlignedAccess.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Core/NoAlias.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Core/PermutationMatrix.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Core/Product.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Core/ProductBase.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Core/Redux.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Core/SelfAdjointView.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Core/StableNorm.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Core/Transpose.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Core/TriangularMatrix.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Eigenvalues/MatrixBaseEigenvalues.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Geometry/EulerAngles.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Geometry/Homogeneous.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Geometry/OrthoMethods.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Geometry/Scaling.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Householder/Householder.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Jacobi/Jacobi.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/LU/Determinant.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/LU/FullPivLU.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/LU/Inverse.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/LU/PartialPivLU.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/QR/ColPivHouseholderQR.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/QR/FullPivHouseholderQR.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/QR/HouseholderQR.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/Sparse/SparseView.h
/home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/ntk/geometry/Eigen/src/SVD/JacobiSVD.h

MatrixBase< Derived > Class Template Reference

Classes

Public Types

Public Member Functions

Static Public Member Functions

Protected Member Functions

Friends

Detailed Description

template<typename Derived> class MatrixBase< Derived >

Member Typedef Documentation

Member Enumeration Documentation

Constructor & Destructor Documentation

Member Function Documentation

Friends And Related Function Documentation

template<typename Derived>
class MatrixBase< Derived >