Classes | |
| class | AlignedBox< _Scalar, _AmbientDim > |
| An axis aligned box. More... | |
| class | AngleAxis< _Scalar > |
| Represents a 3D rotation as a rotation angle around an arbitrary 3D axis. More... | |
| class | Hyperplane< _Scalar, _AmbientDim > |
| A hyperplane. More... | |
| class | ParametrizedLine< _Scalar, _AmbientDim > |
| A parametrized line. More... | |
| class | Quaternion< _Scalar > |
| The quaternion class used to represent 3D orientations and rotations. More... | |
| class | Rotation2D< _Scalar > |
| Represents a rotation/orientation in a 2 dimensional space. More... | |
| class | Scaling< _Scalar, _Dim > |
| Represents a possibly non uniform scaling transformation. More... | |
| class | Transform< _Scalar, _Dim > |
| Represents an homogeneous transformation in a N dimensional space. More... | |
| class | Translation< _Scalar, _Dim > |
| Represents a translation transformation. More... | |
| class | Homogeneous< MatrixType, _Direction > |
| Expression of one (or a set of) homogeneous vector(s). More... | |
Typedefs | |
| typedef AngleAxis< float > | AngleAxisf |
| typedef AngleAxis< double > | AngleAxisd |
| typedef Quaternion< float > | Quaternionf |
| typedef Quaternion< double > | Quaterniond |
| typedef Rotation2D< float > | Rotation2Df |
| typedef Rotation2D< double > | Rotation2Dd |
| typedef Scaling< float, 2 > | Scaling2f |
| typedef Scaling< double, 2 > | Scaling2d |
| typedef Scaling< float, 3 > | Scaling3f |
| typedef Scaling< double, 3 > | Scaling3d |
| typedef Transform< float, 2 > | Transform2f |
| typedef Transform< float, 3 > | Transform3f |
| typedef Transform< double, 2 > | Transform2d |
| typedef Transform< double, 3 > | Transform3d |
| typedef Translation< float, 2 > | Translation2f |
| typedef Translation< double, 2 > | Translation2d |
| typedef Translation< float, 3 > | Translation3f |
| typedef Translation< double, 3 > | Translation3d |
| typedef AngleAxis< float > | AngleAxisf |
| typedef AngleAxis< double > | AngleAxisd |
| typedef Quaternion< float > | Quaternionf |
| typedef Quaternion< double > | Quaterniond |
| typedef Map< Quaternion< float >, 0 > | QuaternionMapf |
| typedef Map< Quaternion < double >, 0 > | QuaternionMapd |
| typedef Map< Quaternion< float > , Aligned > | QuaternionMapAlignedf |
| typedef Map< Quaternion < double >, Aligned > | QuaternionMapAlignedd |
| typedef Rotation2D< float > | Rotation2Df |
| typedef Rotation2D< double > | Rotation2Dd |
| typedef DiagonalMatrix< float, 2 > | AlignedScaling2f |
| typedef DiagonalMatrix< double, 2 > | AlignedScaling2d |
| typedef DiagonalMatrix< float, 3 > | AlignedScaling3f |
| typedef DiagonalMatrix< double, 3 > | AlignedScaling3d |
| typedef Transform< float, 2, Isometry > | Isometry2f |
| typedef Transform< float, 3, Isometry > | Isometry3f |
| typedef Transform< double, 2, Isometry > | Isometry2d |
| typedef Transform< double, 3, Isometry > | Isometry3d |
| typedef Transform< float, 2, Affine > | Affine2f |
| typedef Transform< float, 3, Affine > | Affine3f |
| typedef Transform< double, 2, Affine > | Affine2d |
| typedef Transform< double, 3, Affine > | Affine3d |
| typedef Transform< float, 2, AffineCompact > | AffineCompact2f |
| typedef Transform< float, 3, AffineCompact > | AffineCompact3f |
| typedef Transform< double, 2, AffineCompact > | AffineCompact2d |
| typedef Transform< double, 3, AffineCompact > | AffineCompact3d |
| typedef Transform< float, 2, Projective > | Projective2f |
| typedef Transform< float, 3, Projective > | Projective3f |
| typedef Transform< double, 2, Projective > | Projective2d |
| typedef Transform< double, 3, Projective > | Projective3d |
| typedef Translation< float, 2 > | Translation2f |
| typedef Translation< double, 2 > | Translation2d |
| typedef Translation< float, 3 > | Translation3f |
| typedef Translation< double, 3 > | Translation3d |
Functions | |
| template<typename Derived , typename OtherDerived > | |
| internal::umeyama_transform_matrix_type < Derived, OtherDerived > ::type | umeyama (const MatrixBase< Derived > &src, const MatrixBase< OtherDerived > &dst, bool with_scaling=true) |
| Returns the transformation between two point sets. | |
| Matrix< Scalar, 3, 1 > | MatrixBase::eulerAngles (Index a0, Index a1, Index a2) const |
Typedef Documentation
| typedef Transform<double,2,AffineCompact> AffineCompact2d |
| typedef Transform<float,2,AffineCompact> AffineCompact2f |
| typedef Transform<double,3,AffineCompact> AffineCompact3d |
| typedef Transform<float,3,AffineCompact> AffineCompact3f |
| typedef DiagonalMatrix<double,2> AlignedScaling2d |
| typedef DiagonalMatrix<float, 2> AlignedScaling2f |
| typedef DiagonalMatrix<double,3> AlignedScaling3d |
| typedef DiagonalMatrix<float, 3> AlignedScaling3f |
| typedef AngleAxis<double> AngleAxisd |
double precision angle-axis type
| typedef AngleAxis<double> AngleAxisd |
double precision angle-axis type
| typedef AngleAxis<float> AngleAxisf |
single precision angle-axis type
| typedef AngleAxis<float> AngleAxisf |
single precision angle-axis type
| typedef Transform<double,2,Isometry> Isometry2d |
| typedef Transform<float,2,Isometry> Isometry2f |
| typedef Transform<double,3,Isometry> Isometry3d |
| typedef Transform<float,3,Isometry> Isometry3f |
| typedef Transform<double,2,Projective> Projective2d |
| typedef Transform<float,2,Projective> Projective2f |
| typedef Transform<double,3,Projective> Projective3d |
| typedef Transform<float,3,Projective> Projective3f |
| typedef Quaternion<double> Quaterniond |
double precision quaternion type
| typedef Quaternion<double> Quaterniond |
double precision quaternion type
| typedef Quaternion<float> Quaternionf |
single precision quaternion type
| typedef Quaternion<float> Quaternionf |
single precision quaternion type
| typedef Map<Quaternion<double>, Aligned> QuaternionMapAlignedd |
Map a 16-bits aligned array of double precision scalars as a quaternion
| typedef Map<Quaternion<float>, Aligned> QuaternionMapAlignedf |
Map a 16-bits aligned array of double precision scalars as a quaternion
| typedef Map<Quaternion<double>, 0> QuaternionMapd |
Map an unaligned array of double precision scalar as a quaternion
| typedef Map<Quaternion<float>, 0> QuaternionMapf |
Map an unaligned array of single precision scalar as a quaternion
| typedef Rotation2D<double> Rotation2Dd |
double precision 2D rotation type
| typedef Rotation2D<double> Rotation2Dd |
double precision 2D rotation type
| typedef Rotation2D<float> Rotation2Df |
single precision 2D rotation type
| typedef Rotation2D<float> Rotation2Df |
single precision 2D rotation type
| typedef Transform<double,2> Transform2d |
| typedef Transform<float,2> Transform2f |
| typedef Transform<double,3> Transform3d |
| typedef Transform<float,3> Transform3f |
| typedef Translation<double,2> Translation2d |
| typedef Translation<double,2> Translation2d |
| typedef Translation<float, 2> Translation2f |
| typedef Translation<float, 2> Translation2f |
| typedef Translation<double,3> Translation3d |
| typedef Translation<double,3> Translation3d |
| typedef Translation<float, 3> Translation3f |
| typedef Translation<float, 3> Translation3f |
Function Documentation
| Matrix< typename MatrixBase< Derived >::Scalar, 3, 1 > MatrixBase< Derived >::eulerAngles | ( | Index | a0, | |
| Index | a1, | |||
| Index | a2 | |||
| ) | const [inline, inherited] |
- Returns:
- the Euler-angles of the rotation matrix
*thisusing the convention defined by the triplet (a0,a1,a2)
Each of the three parameters a0,a1,a2 represents the respective rotation axis as an integer in {0,1,2}. For instance, in:
Vector3f ea = mat.eulerAngles(2, 0, 2);
"2" represents the z axis and "0" the x axis, etc. The returned angles are such that we have the following equality:
mat == AngleAxisf(ea[0], Vector3f::UnitZ()) * AngleAxisf(ea[1], Vector3f::UnitX()) * AngleAxisf(ea[2], Vector3f::UnitZ());
This corresponds to the right-multiply conventions (with right hand side frames).
| internal::umeyama_transform_matrix_type<Derived, OtherDerived>::type umeyama | ( | const MatrixBase< Derived > & | src, | |
| const MatrixBase< OtherDerived > & | dst, | |||
| bool | with_scaling = true | |||
| ) |
Returns the transformation between two point sets.
The algorithm is based on: "Least-squares estimation of transformation parameters between two point patterns", Shinji Umeyama, PAMI 1991, DOI: 10.1109/34.88573
It estimates parameters 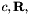 and
and 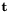 such that
such that
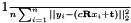
is minimized.
The algorithm is based on the analysis of the covariance matrix 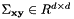 of the input point sets
of the input point sets 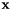 and
and 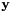 where
where 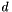 is corresponding to the dimension (which is typically small). The analysis is involving the SVD having a complexity of
is corresponding to the dimension (which is typically small). The analysis is involving the SVD having a complexity of 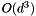 though the actual computational effort lies in the covariance matrix computation which has an asymptotic lower bound of
though the actual computational effort lies in the covariance matrix computation which has an asymptotic lower bound of 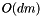 when the input point sets have dimension
when the input point sets have dimension 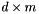 .
.
Currently the method is working only for floating point matrices.
- Parameters:
-
src Source points 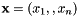 .
. dst Destination points 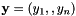 .
. with_scaling Sets 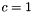 when
when falseis passed.
- Returns:
- The homogeneous transformation
minimizing the resudiual above. This transformation is always returned as an Eigen::Matrix.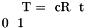
 1.7.1
1.7.1