Public Types | Public Member Functions | Protected Member Functions | Protected Attributes

JacobiRotation< Scalar > Class Template Reference

Rotation given by a cosine-sine pair. More...

#include <Jacobi.h>

List of all members.

Public Types

typedef NumTraits< Scalar >::Real RealScalar

Public Member Functions

 JacobiRotation ()
 JacobiRotation (const Scalar &c, const Scalar &s)
Scalar & c ()
Scalar c () const
Scalar & s ()
Scalar s () const
JacobiRotation operator* (const JacobiRotation &other)
JacobiRotation transpose () const
JacobiRotation adjoint () const
template<typename Derived >
bool makeJacobi (const MatrixBase< Derived > &, typename Derived::Index p, typename Derived::Index q)
bool makeJacobi (RealScalar x, Scalar y, RealScalar z)
void makeGivens (const Scalar &p, const Scalar &q, Scalar *z=0)

Protected Member Functions

void makeGivens (const Scalar &p, const Scalar &q, Scalar *z, internal::true_type)
void makeGivens (const Scalar &p, const Scalar &q, Scalar *z, internal::false_type)

Protected Attributes

Scalar m_c
Scalar m_s

Detailed Description

template<typename Scalar>
class JacobiRotation< Scalar >

Rotation given by a cosine-sine pair.

This class represents a Jacobi or Givens rotation. This is a 2D rotation in the plane J of angle 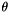$ \theta $ defined by its cosine c and sine s as follow: 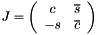$ J = \left ( \begin{array}{cc} c & \overline s \\ -s & \overline c \end{array} \right ) $

You can apply the respective counter-clockwise rotation to a column vector v by applying its adjoint on the left: 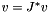$ v = J^* v $ that translates to the following Eigen code: 

 v.applyOnTheLeft(J.adjoint());
See also:
MatrixBase::applyOnTheLeft(), MatrixBase::applyOnTheRight()

Member Typedef Documentation

template<typename Scalar>
typedef NumTraits<Scalar>::Real JacobiRotation< Scalar >::RealScalar

Constructor & Destructor Documentation

template<typename Scalar>
JacobiRotation< Scalar >::JacobiRotation (  )  [inline]

Default constructor without any initialization.

template<typename Scalar>
JacobiRotation< Scalar >::JacobiRotation ( const Scalar &  c,
const Scalar &  s 
) [inline]

Construct a planar rotation from a cosine-sine pair (c, s).

Member Function Documentation

template<typename Scalar>
JacobiRotation JacobiRotation< Scalar >::adjoint (  )  const [inline]

Returns the adjoint transformation

template<typename Scalar>
Scalar JacobiRotation< Scalar >::c (  )  const [inline]
template<typename Scalar>
Scalar& JacobiRotation< Scalar >::c (  )  [inline]
template<typename Scalar >
void JacobiRotation< Scalar >::makeGivens ( const Scalar &  p,
const Scalar &  q,
Scalar *  z = 0 
)

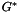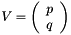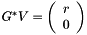Makes *this as a Givens rotation G such that applying $ G^* $ to the left of the vector $ V = \left ( \begin{array}{c} p \\ q \end{array} \right )$ yields: $ G^* V = \left ( \begin{array}{c} r \\ 0 \end{array} \right )$.

The value of z is returned if z is not null (the default is null). Also note that G is built such that the cosine is always real.

Example: 

 Output: 


This function implements the continuous Givens rotation generation algorithm found in Anderson (2000), Discontinuous Plane Rotations and the Symmetric Eigenvalue Problem. LAPACK Working Note 150, University of Tennessee, UT-CS-00-454, December 4, 2000.


See also:
MatrixBase::applyOnTheLeft(), MatrixBase::applyOnTheRight() 













template<typename Scalar > 

      

        

          void JacobiRotation< Scalar >::makeGivens 
          (
          const Scalar & 
           p, 
        

        

          
          
          const Scalar & 
           q, 
        

        

          
          
          Scalar * 
           z, 
        

        

          
          
          internal::true_type 
           
        

        

          
          )
           [protected]
        

      

















template<typename Scalar > 

      

        

          void JacobiRotation< Scalar >::makeGivens 
          (
          const Scalar & 
           p, 
        

        

          
          
          const Scalar & 
           q, 
        

        

          
          
          Scalar * 
           z, 
        

        

          
          
          internal::false_type 
           
        

        

          
          )
           [protected]
        

      

















template<typename Scalar > 

      

        

          bool JacobiRotation< Scalar >::makeJacobi 
          (
          RealScalar 
           x, 
        

        

          
          
          Scalar 
           y, 
        

        

          
          
          RealScalar 
           z 
        

        

          
          )
          
        

      






Makes *this as a Jacobi rotation J such that applying J on both the right and left sides of the selfadjoint 2x2 matrix 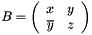$ B = \left ( \begin{array}{cc} x & y \\ \overline y & z \end{array} \right )$ yields a diagonal matrix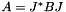 $ A = J^* B J $


See also:
MatrixBase::makeJacobi(const MatrixBase<Derived>&, Index, Index), MatrixBase::applyOnTheLeft(), MatrixBase::applyOnTheRight() 













template<typename Scalar > 



template<typename Derived > 

      

        

          bool JacobiRotation< Scalar >::makeJacobi 
          (
          const MatrixBase< Derived > & 
           m, 
        

        

          
          
          typename Derived::Index 
           p, 
        

        

          
          
          typename Derived::Index 
           q 
        

        

          
          )
           [inline]
        

      






Makes *this as a Jacobi rotation J such that applying J on both the right and left sides of the 2x2 selfadjoint matrix 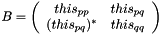$ B = \left ( \begin{array}{cc} \text{this}_{pp} & \text{this}_{pq} \\ (\text{this}_{pq})^* & \text{this}_{qq} \end{array} \right )$ yields a diagonal matrix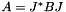 $ A = J^* B J $


Example: 


 Output: 


See also:
JacobiRotation::makeJacobi(RealScalar, Scalar, RealScalar), MatrixBase::applyOnTheLeft(), MatrixBase::applyOnTheRight() 













template<typename Scalar> 

      

        

          JacobiRotation JacobiRotation< Scalar >::operator* 
          (
          const JacobiRotation< Scalar > & 
           other
           ) 
           [inline]
        

      






Concatenates two planar rotation 













template<typename Scalar> 

      

        

          Scalar& JacobiRotation< Scalar >::s 
          (
          
           ) 
           [inline]
        

      

















template<typename Scalar> 

      

        

          Scalar JacobiRotation< Scalar >::s 
          (
          
           ) 
           const [inline]
        

      

















template<typename Scalar> 

      

        

          JacobiRotation JacobiRotation< Scalar >::transpose 
          (
          
           ) 
           const [inline]
        

      






Returns the transposed transformation 







Member Data Documentation








template<typename Scalar> 

      

        

          Scalar JacobiRotation< Scalar >::m_c [protected]
        

      

















template<typename Scalar> 

      

        

          Scalar JacobiRotation< Scalar >::m_s [protected]
        

      











The documentation for this class was generated from the following file:



Generated on Thu Dec 1 2011 12:54:27 for HUMIM Tracker by 

doxygen 1.7.1