Householder rank-revealing QR decomposition of a matrix with column-pivoting. More...

#include <ColPivHouseholderQR.h>

Public Types
enum	{ RowsAtCompileTime = MatrixType::RowsAtCompileTime, ColsAtCompileTime = MatrixType::ColsAtCompileTime, Options = MatrixType::Options, MaxRowsAtCompileTime = MatrixType::MaxRowsAtCompileTime, MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime }
typedef _MatrixType	MatrixType
typedef MatrixType::Scalar	Scalar
typedef MatrixType::RealScalar	RealScalar
typedef MatrixType::Index	Index
typedef Matrix< Scalar, RowsAtCompileTime, RowsAtCompileTime, Options, MaxRowsAtCompileTime, MaxRowsAtCompileTime >	MatrixQType
typedef internal::plain_diag_type < MatrixType >::type	HCoeffsType
typedef PermutationMatrix < ColsAtCompileTime, MaxColsAtCompileTime >	PermutationType
typedef internal::plain_row_type < MatrixType, Index >::type	IntRowVectorType
typedef internal::plain_row_type < MatrixType >::type	RowVectorType
typedef internal::plain_row_type < MatrixType, RealScalar > ::type	RealRowVectorType
typedef HouseholderSequence < MatrixType, HCoeffsType > ::ConjugateReturnType	HouseholderSequenceType
Public Member Functions
	ColPivHouseholderQR ()
	Default Constructor.
	ColPivHouseholderQR (Index rows, Index cols)
	Default Constructor with memory preallocation.
	ColPivHouseholderQR (const MatrixType &matrix)
template<typename Rhs >
const internal::solve_retval < ColPivHouseholderQR, Rhs >	solve (const MatrixBase< Rhs > &b) const
HouseholderSequenceType	householderQ (void) const
const MatrixType &	matrixQR () const
ColPivHouseholderQR &	compute (const MatrixType &matrix)
const PermutationType &	colsPermutation () const
MatrixType::RealScalar	absDeterminant () const
MatrixType::RealScalar	logAbsDeterminant () const
Index	rank () const
Index	dimensionOfKernel () const
bool	isInjective () const
bool	isSurjective () const
bool	isInvertible () const
const internal::solve_retval < ColPivHouseholderQR, typename MatrixType::IdentityReturnType >	inverse () const
Index	rows () const
Index	cols () const
const HCoeffsType &	hCoeffs () const
ColPivHouseholderQR &	setThreshold (const RealScalar &threshold)
ColPivHouseholderQR &	setThreshold (Default_t)
RealScalar	threshold () const
Index	nonzeroPivots () const
RealScalar	maxPivot () const
Protected Attributes
MatrixType	m_qr
HCoeffsType	m_hCoeffs
PermutationType	m_colsPermutation
IntRowVectorType	m_colsTranspositions
RowVectorType	m_temp
RealRowVectorType	m_colSqNorms
bool	m_isInitialized
bool	m_usePrescribedThreshold
RealScalar	m_prescribedThreshold
RealScalar	m_maxpivot
Index	m_nonzero_pivots
Index	m_det_pq

Detailed Description

template<typename _MatrixType>
class ColPivHouseholderQR< _MatrixType >

Householder rank-revealing QR decomposition of a matrix with column-pivoting.

Parameters:

MatrixType

the type of the matrix of which we are computing the QR decomposition

This class performs a rank-revealing QR decomposition of a matrix A into matrices P, Q and R such that

$\mathbf{A} \, \mathbf{P} = \mathbf{Q} \, \mathbf{R}$

by using Householder transformations. Here, P is a permutation matrix, Q a unitary matrix and R an upper triangular matrix.

This decomposition performs column pivoting in order to be rank-revealing and improve numerical stability. It is slower than HouseholderQR, and faster than FullPivHouseholderQR.

See also:: MatrixBase::colPivHouseholderQr()

Member Typedef Documentation

template<typename _MatrixType>

typedef internal::plain_diag_type<MatrixType>::type ColPivHouseholderQR< _MatrixType >::HCoeffsType

template<typename _MatrixType>

typedef HouseholderSequence<MatrixType,HCoeffsType>::ConjugateReturnType ColPivHouseholderQR< _MatrixType >::HouseholderSequenceType

template<typename _MatrixType>

typedef MatrixType::Index ColPivHouseholderQR< _MatrixType >::Index

template<typename _MatrixType>

typedef internal::plain_row_type<MatrixType, Index>::type ColPivHouseholderQR< _MatrixType >::IntRowVectorType

template<typename _MatrixType>

typedef Matrix<Scalar, RowsAtCompileTime, RowsAtCompileTime, Options, MaxRowsAtCompileTime, MaxRowsAtCompileTime> ColPivHouseholderQR< _MatrixType >::MatrixQType

template<typename _MatrixType>

typedef _MatrixType ColPivHouseholderQR< _MatrixType >::MatrixType

template<typename _MatrixType>

typedef PermutationMatrix<ColsAtCompileTime, MaxColsAtCompileTime> ColPivHouseholderQR< _MatrixType >::PermutationType

template<typename _MatrixType>

typedef internal::plain_row_type<MatrixType, RealScalar>::type ColPivHouseholderQR< _MatrixType >::RealRowVectorType

template<typename _MatrixType>

typedef MatrixType::RealScalar ColPivHouseholderQR< _MatrixType >::RealScalar

template<typename _MatrixType>

typedef internal::plain_row_type<MatrixType>::type ColPivHouseholderQR< _MatrixType >::RowVectorType

template<typename _MatrixType>

typedef MatrixType::Scalar ColPivHouseholderQR< _MatrixType >::Scalar

Member Enumeration Documentation

template<typename _MatrixType>

anonymous enum

Enumerator:

RowsAtCompileTime
ColsAtCompileTime
Options
MaxRowsAtCompileTime
MaxColsAtCompileTime

Constructor & Destructor Documentation

template<typename _MatrixType>

ColPivHouseholderQR< _MatrixType >::ColPivHouseholderQR ( ) [inline]

Default Constructor.

The default constructor is useful in cases in which the user intends to perform decompositions via ColPivHouseholderQR::compute(const MatrixType&).

template<typename _MatrixType>

ColPivHouseholderQR< _MatrixType >::ColPivHouseholderQR	(	Index	rows,
		Index	cols
	)			`[inline]`

Default Constructor with memory preallocation.

Like the default constructor but with preallocation of the internal data according to the specified problem size.

See also:: ColPivHouseholderQR()

template<typename _MatrixType>

ColPivHouseholderQR< _MatrixType >::ColPivHouseholderQR ( const MatrixType & matrix ) [inline]

Member Function Documentation

template<typename MatrixType >

MatrixType::RealScalar ColPivHouseholderQR< MatrixType >::absDeterminant ( ) const

Returns:: the absolute value of the determinant of the matrix of which *this is the QR decomposition. It has only linear complexity (that is, O(n) where n is the dimension of the square matrix) as the QR decomposition has already been computed.

Note:: This is only for square matrices.

Warning:: a determinant can be very big or small, so for matrices of large enough dimension, there is a risk of overflow/underflow. One way to work around that is to use logAbsDeterminant() instead.

See also:: logAbsDeterminant(), MatrixBase::determinant()

template<typename _MatrixType>

Index ColPivHouseholderQR< _MatrixType >::cols ( void ) const [inline]

template<typename _MatrixType>

const PermutationType& ColPivHouseholderQR< _MatrixType >::colsPermutation ( ) const [inline]

template<typename MatrixType >

ColPivHouseholderQR< MatrixType > & ColPivHouseholderQR< MatrixType >::compute ( const MatrixType & matrix )

template<typename _MatrixType>

Index ColPivHouseholderQR< _MatrixType >::dimensionOfKernel ( ) const [inline]

Returns:: the dimension of the kernel of the matrix of which *this is the QR decomposition.

Note:: This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

template<typename _MatrixType>

const HCoeffsType& ColPivHouseholderQR< _MatrixType >::hCoeffs ( ) const [inline]

template<typename MatrixType >

ColPivHouseholderQR< MatrixType >::HouseholderSequenceType ColPivHouseholderQR< MatrixType >::householderQ ( void ) const

Returns:: the matrix Q as a sequence of householder transformations

template<typename _MatrixType>

const internal::solve_retval<ColPivHouseholderQR, typename MatrixType::IdentityReturnType> ColPivHouseholderQR< _MatrixType >::inverse ( void ) const [inline]

Returns:: the inverse of the matrix of which *this is the QR decomposition.

Note:: If this matrix is not invertible, the returned matrix has undefined coefficients. Use isInvertible() to first determine whether this matrix is invertible.

template<typename _MatrixType>

bool ColPivHouseholderQR< _MatrixType >::isInjective ( ) const [inline]

Returns:: true if the matrix of which *this is the QR decomposition represents an injective linear map, i.e. has trivial kernel; false otherwise.

Note:: This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

template<typename _MatrixType>

bool ColPivHouseholderQR< _MatrixType >::isInvertible ( ) const [inline]

Returns:: true if the matrix of which *this is the QR decomposition is invertible.

Note:: This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

template<typename _MatrixType>

bool ColPivHouseholderQR< _MatrixType >::isSurjective ( ) const [inline]

Returns:: true if the matrix of which *this is the QR decomposition represents a surjective linear map; false otherwise.

Note:: This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

template<typename MatrixType >

MatrixType::RealScalar ColPivHouseholderQR< MatrixType >::logAbsDeterminant ( ) const

Returns:: the natural log of the absolute value of the determinant of the matrix of which *this is the QR decomposition. It has only linear complexity (that is, O(n) where n is the dimension of the square matrix) as the QR decomposition has already been computed.

Note:: This is only for square matrices.; This method is useful to work around the risk of overflow/underflow that's inherent to determinant computation.

See also:: absDeterminant(), MatrixBase::determinant()

template<typename _MatrixType>

const MatrixType& ColPivHouseholderQR< _MatrixType >::matrixQR ( ) const [inline]

Returns:: a reference to the matrix where the Householder QR decomposition is stored

template<typename _MatrixType>

RealScalar ColPivHouseholderQR< _MatrixType >::maxPivot ( ) const [inline]

Returns:: the absolute value of the biggest pivot, i.e. the biggest diagonal coefficient of U.

template<typename _MatrixType>

Index ColPivHouseholderQR< _MatrixType >::nonzeroPivots ( ) const [inline]

Returns:: the number of nonzero pivots in the QR decomposition. Here nonzero is meant in the exact sense, not in a fuzzy sense. So that notion isn't really intrinsically interesting, but it is still useful when implementing algorithms.

See also:: rank()

template<typename _MatrixType>

Index ColPivHouseholderQR< _MatrixType >::rank ( ) const [inline]

Returns:: the rank of the matrix of which *this is the QR decomposition.

Note:: This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

template<typename _MatrixType>

Index ColPivHouseholderQR< _MatrixType >::rows ( void ) const [inline]

template<typename _MatrixType>

ColPivHouseholderQR& ColPivHouseholderQR< _MatrixType >::setThreshold ( Default_t ) [inline]

Allows to come back to the default behavior, letting Eigen use its default formula for determining the threshold.

You should pass the special object Eigen::Default as parameter here.

 qr.setThreshold(Eigen::Default);

See the documentation of setThreshold(const RealScalar&).

template<typename _MatrixType>

ColPivHouseholderQR& ColPivHouseholderQR< _MatrixType >::setThreshold ( const RealScalar & threshold ) [inline]

Allows to prescribe a threshold to be used by certain methods, such as rank(), who need to determine when pivots are to be considered nonzero. This is not used for the QR decomposition itself.

When it needs to get the threshold value, Eigen calls threshold(). By default, this uses a formula to automatically determine a reasonable threshold. Once you have called the present method setThreshold(const RealScalar&), your value is used instead.

Parameters:

threshold

The new value to use as the threshold.

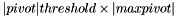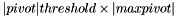A pivot will be considered nonzero if its absolute value is strictly greater than $\vert pivot \vert \leqslant threshold \times \vert maxpivot \vert$ where maxpivot is the biggest pivot.