Namespaces | |
| namespace | detail |
| namespace | obsolete |
Classes | |
| class | Simplex |
| class | VoronoiSimplexSolverPolicy |
| class | Box |
| class | Capsule |
| class | Cone |
| class | Cylinder |
| class | Ellipsoid |
| class | Point |
| class | Sphere |
Functions | |
| template<typename transform_type , typename support_functor1 , typename support_functor2 , typename simplex_solver_policy > | |
| void | compute_closest_points (transform_type const &transform_A, support_functor1 const &support_function_A, transform_type const &transform_B, support_functor2 const &support_function_B, typename transform_type::vector3_type &p_a, typename transform_type::vector3_type &p_b, typename transform_type::value_type &distance, size_t &iterations, size_t &status, typename transform_type::value_type const &absolute_tolerance, typename transform_type::value_type const &relative_tolerance, typename transform_type::value_type const &stagnation_tolerance, size_t const &max_iterations, simplex_solver_policy const &) |
| template<typename transform_type , typename support_functor1 , typename support_functor2 > | |
| void | compute_closest_points (transform_type const &transform_A, support_functor1 const &A, transform_type const &transform_B, support_functor2 const &B, typename transform_type::vector3_type &p_a, typename transform_type::vector3_type &p_b, typename transform_type::value_type &distance, size_t &status) |
| std::string | get_status_message (size_t const &code) |
| template<typename V > | |
| bool | is_point_in_simplex (V const &p, Simplex< V > const &S) |
| template<typename V > | |
| void | add_point_to_simplex (V const &p, V const &p_a, V const &p_b, Simplex< V > &S) |
| template<typename V > | |
| size_t | dimension (Simplex< V > const &S) |
| template<typename V > | |
| bool | is_full_simplex (Simplex< V > const &S) |
| void | get_used_indices (int const &bitmask, size_t &idx_A, int &bit_A) |
| void | get_used_indices (int const &bitmask, size_t &idx_A, int &bit_A, size_t &idx_B, int &bit_B) |
| void | get_used_indices (int const &bitmask, size_t &idx_A, int &bit_A, size_t &idx_B, int &bit_B, size_t &idx_C, int &bit_C) |
Variables | |
| size_t const | ABSOLUTE_CONVERGENCE = 0u |
| size_t const | RELATIVE_CONVERGENCE = 1u |
| size_t const | STAGNATION = 2u |
| size_t const | INTERSECTION = 3u |
| size_t const | EXCEEDED_MAX_ITERATIONS_LIMIT = 4u |
| size_t const | ITERATING = 5u |
| size_t const | NON_DESCEND_DIRECTION = 6u |
| size_t const | SIMPLEX_EXPANSION_FAILED = 7u |
| size_t const | LOWER_ERROR_BOUND_CONVERGENCE = 8u |
Function Documentation
| void OpenTissue::gjk::add_point_to_simplex | ( | V const & | p, | |
| V const & | p_a, | |||
| V const & | p_b, | |||
| Simplex< V > & | S | |||
| ) | [inline] |
- Parameters:
-
p The point to be added to the simplex. It is assumed implicitly that this point is linear independent of the points already contained in the simplex. p_a A corresponding point from set A. p_b A corresponding point from set B. S The simplex where the point should be added.
| void OpenTissue::gjk::compute_closest_points | ( | transform_type const & | transform_A, | |
| support_functor1 const & | support_function_A, | |||
| transform_type const & | transform_B, | |||
| support_functor2 const & | support_function_B, | |||
| typename transform_type::vector3_type & | p_a, | |||
| typename transform_type::vector3_type & | p_b, | |||
| typename transform_type::value_type & | distance, | |||
| size_t & | iterations, | |||
| size_t & | status, | |||
| typename transform_type::value_type const & | absolute_tolerance, | |||
| typename transform_type::value_type const & | relative_tolerance, | |||
| typename transform_type::value_type const & | stagnation_tolerance, | |||
| size_t const & | max_iterations, | |||
| simplex_solver_policy const & | ||||
| ) | [inline] |
Compute Closest Points and Distance between two Convex Sets. This function uses an iterative algorithm. In each iteration a simplex is updated to best approximate the Minikowsky difference between two given convex objects 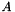 and
and 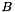 . The Minikowsky Difference set is implicitly represented by the support functions of the two objects. The following text tries to give a short introduction to the concepts.
. The Minikowsky Difference set is implicitly represented by the support functions of the two objects. The following text tries to give a short introduction to the concepts.
Given two objects represented by the two sets 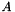 and
and 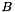 then the two objects overlap if there exist at least one
then the two objects overlap if there exist at least one 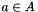 and one
and one 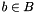 such that
such that
![\[ a - b = 0 \]](form_172.png)
Thus one way to test for intersection of the two objects is to form the set
![\[ A \ominus B = \{ a - b | a \in A, b \in B \} \]](form_173.png)
and see if
![\[ 0 \in A \ominus B \]](form_174.png)
The set 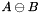 is called the Minokowsky difference. Clearly if the two objects are separated one must have that
is called the Minokowsky difference. Clearly if the two objects are separated one must have that
![\[ a - b \neq 0 \]](form_176.png)
holds for all 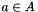 and all
and all 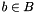 , or equivalently that
, or equivalently that
![\[ 0 \notin A \ominus B \]](form_177.png)
Assume that the two objects are separated then one may want to know the minimum distance between the two objects. That is one wants to find
![\[ (a^*, b^*) = \min_{a \in A, b \in B} \norm{(a-b)} = \min_{y \in A \ominus B} \norm{(y)} \]](form_178.png)
or equivalently
![\[ y^* = \min_{y \in A \ominus B} \norm{(y)} \]](form_179.png)
Thus seeking the minimum distance between the two object is equivalent to finding the minimum norm point in the set 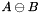 . Or said differently to find a point in
. Or said differently to find a point in 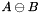 that is closest to zero.
that is closest to zero.
Observe that if we find such a point 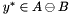 then we implicitly also know the two closest points between
then we implicitly also know the two closest points between 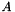 and
and 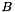 , since
, since 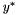 is defined as
is defined as 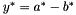 for some
for some 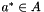 and some
and some 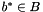 .
.
The important thing to realise is that the problem of finding the minimum distance between two sets 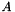 and
and 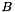 is equivalent to the problem of finding the distance between a point and the set
is equivalent to the problem of finding the distance between a point and the set 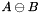 . Thus we have replaced the original problem with a simple one.
. Thus we have replaced the original problem with a simple one.
One should notice that the solution may not be unique since there could exist multiple 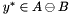 that yield the same minimum distance. Further a solution may not exist if
that yield the same minimum distance. Further a solution may not exist if 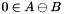 .
.
- Parameters:
-
transform_A A coordinate (a rigid body) transformation that is used to place first convex set. support_function_A A support function describing the shape of the first convex set. transform_B A coordinate (a rigid body) transformation that is used to place second convex set. support_function_B A support function describing the shape of the second convex set. p_a Upon return this argument holds the closest point on the first convex set. p_b Upon return this argument holds the closest point on the second convex set. distance Upon return this argument holds the distance between the point and the convex set. iterations Upon return this argument holds the number of iterations used. status The status code of the algorithm. absolute_tolerance relative_tolerance stagnation_tolerance max_iterations
- Template Parameters:
-
transform_type This template argument provides a coordinate transformation type. The type must support that one can query a quaternion representation of the orientation and a vector3_type representation of the translation. The OpenTissue CoordSys template class can be used for creating the type. simplex_solver_policy This template argument provides the algorithm with a policy for how to deal with the simplex approximation.
| void OpenTissue::gjk::compute_closest_points | ( | transform_type const & | transform_A, | |
| support_functor1 const & | A, | |||
| transform_type const & | transform_B, | |||
| support_functor2 const & | B, | |||
| typename transform_type::vector3_type & | p_a, | |||
| typename transform_type::vector3_type & | p_b, | |||
| typename transform_type::value_type & | distance, | |||
| size_t & | status | |||
| ) | [inline] |
Lazy Man's Version. This function uses presets for parameters that control the algorithm.
| size_t OpenTissue::gjk::dimension | ( | Simplex< V > const & | S | ) | [inline] |
The Dimension of the Simplex.
- Parameters:
-
S The simplex.
- Returns:
- The dimension of the simplex, this is defined as the cardinality of the simplex vertex set.
| std::string OpenTissue::gjk::get_status_message | ( | size_t const & | code | ) | [inline] |
Get Status Message. This function decodes an given status code value into a user friendly and human readable text string. The text string may be convenient for displaying status messages in a log or on screen for an end-user.
- Parameters:
-
code The value of an error code.
- Returns:
- A textual and human readable status message string.
| void OpenTissue::gjk::get_used_indices | ( | int const & | bitmask, | |
| size_t & | idx_A, | |||
| int & | bit_A, | |||
| size_t & | idx_B, | |||
| int & | bit_B | |||
| ) | [inline] |
Get First Two Used Indices in Simplex. This function will determine the entry of the first two used simplex vertices.
- Parameters:
-
bitmask A simplex bitmask indicating usage of simplex vertices. idx_A Upon return this argument holds the first entry. bit_A Upon return this argument holds the bit-flag of the first used entry. idx_B Upon return this argument holds the second entry. bit_B Upon return this argument holds the bit-flag of the second used entry.
| void OpenTissue::gjk::get_used_indices | ( | int const & | bitmask, | |
| size_t & | idx_A, | |||
| int & | bit_A, | |||
| size_t & | idx_B, | |||
| int & | bit_B, | |||
| size_t & | idx_C, | |||
| int & | bit_C | |||
| ) | [inline] |
Get First Three Used Indices in Simplex. This function will determine the entry of the first three used simplex vertices.
- Parameters:
-
bitmask A simplex bitmask indicating usage of simplex vertices. idx_A Upon return this argument holds the first entry. bit_A Upon return this argument holds the bit-flag of the first used entry. idx_B Upon return this argument holds second the entry. bit_B Upon return this argument holds the bit-flag of the second used entry. idx_C Upon return this argument holds the third entry. bit_C Upon return this argument holds the bit-flag of the third used entry.
| void OpenTissue::gjk::get_used_indices | ( | int const & | bitmask, | |
| size_t & | idx_A, | |||
| int & | bit_A | |||
| ) | [inline] |
Get First Used Index in Simplex. This function will determine the entry of the first used simplex vertex.
- Parameters:
-
bitmask A simplex bitmask indicating usage of simplex vertices. idx_A Upon return this argument holds the entry. bit_A Upon return this argument holds the bit-flag of the first used entry.
| bool OpenTissue::gjk::is_full_simplex | ( | Simplex< V > const & | S | ) | [inline] |
Test If Simplex is Full. A full simplex is one where all vertices are in use. In our case it means that we got a tetrahedron with 4 vertices.
- Parameters:
-
S The simplex.
- Returns:
- If the simplex got four vertices then the return value is true otherwise it is false.
| bool OpenTissue::gjk::is_point_in_simplex | ( | V const & | p, | |
| Simplex< V > const & | S | |||
| ) | [inline] |
Test if point is in Simplex.
- Parameters:
-
p The point that should be tested for containment. It is assumed that the point is a support point from a support function. S The simplex to test against.
- Returns:
- If p is in the specified simplex then the return value is true otherwise it is false.
Variable Documentation
| size_t const OpenTissue::gjk::ABSOLUTE_CONVERGENCE = 0u |
Absolute convergence status code. This means that the absolute function value has dropped below a given threshold value. Given the current iterate 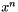 then the test is
then the test is
![\[ f(x^n) < \varepsilon, \]](form_187.png)
where 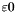 is a user specified test-threshold. In case of minimization the test could also be for a stationary point. The test would then be
is a user specified test-threshold. In case of minimization the test could also be for a stationary point. The test would then be
![\[ | \nabla f(x^n) | < \varepsilon, \]](form_189.png)
| size_t const OpenTissue::gjk::EXCEEDED_MAX_ITERATIONS_LIMIT = 4u |
Exceeded maximum iterations limit status code.
| size_t const OpenTissue::gjk::INTERSECTION = 3u |
Intersection status code.
| size_t const OpenTissue::gjk::ITERATING = 5u |
Iterating status code. This status code basically means that one got an unexpected exit. It should never happen, but if it does this is a clear indication of an internal error.
| size_t const OpenTissue::gjk::LOWER_ERROR_BOUND_CONVERGENCE = 8u |
Relative Convergene by Lower Error Bound.
| size_t const OpenTissue::gjk::NON_DESCEND_DIRECTION = 6u |
Non-descend status code. This status code is returned if an iteration is encountered where the closest distance has increased.
| size_t const OpenTissue::gjk::RELATIVE_CONVERGENCE = 1u |
Relative convergence status code. This means that the relative improvement in function value has dropped below a given threshold value. Given the current iterate 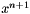 and the previous iterate
and the previous iterate 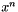 then the test is
then the test is
![\[ \frac{| f(x^{n+1}) - f(x^n) |}{|f(x^n)|} < \varepsilon, \]](form_192.png)
where 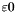 is a user specified test-threshold.
is a user specified test-threshold.
| size_t const OpenTissue::gjk::SIMPLEX_EXPANSION_FAILED = 7u |
Simplex Expansion Failure. This status code is returned if during an iteration no new points can be added to the current simplex.
| size_t const OpenTissue::gjk::STAGNATION = 2u |
Stagnation status code. Stagnation means that the maximum difference between the components of a new iterate and the old iterate dropped below some small threshold value. Basically it means that the two iterates are nearly the same and no progress have been made by the numerical method used.
 1.7.1
1.7.1