#include <gjk_simplex.h>
Public Types | |
| typedef vector3_type::value_traits | value_traits |
| typedef vector3_type::value_type | real_type |
Public Member Functions | |
| Simplex () | |
Public Attributes | |
| int | m_bitmask |
| vector3_type | m_v [4] |
| The simplex vertices. | |
| real_type | m_w [4] |
| Barycentric coordinates for the closest point on the simplex wrt. the simplex vertices. | |
| vector3_type | m_a [4] |
| The support points from object A corresponding to the simplex vertices. | |
| vector3_type | m_b [4] |
| The support points from object B corresponding to the simplex vertices. | |
Detailed Description
template<typename vector3_type>
class OpenTissue::gjk::Simplex< vector3_type >
Simplex Type. This class defines a minimal set of data that defines a simplex. The class is specifically tailored to be used in the GJK algorithm. That means it is limited completely to a singleton simplex in a three dimensional space.
Further the class contains storage for barycentric coordinates and the original support points used to generate the simplex vertices.
Notice that the barycentric coordinates are really only needed when one wants to re-construct the two closest points between two convex sets. This is explained in detail below. In the general distance between point and convex set algorithm there is no need for these coordinates. However, for our specific purpose we need to store them.
The simplex vertices are obtained from a support function for the Minikowsky difference between two convex point sets 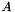 and
and 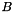 .
.
The Minikowsky Difference is defined as
![\[ A \ominus B = \{a-b | a \in A, b \in B \} \]](form_193.png)
One can show that the support function, 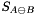 , of the Minikowsky Difference can be evaluated as
, of the Minikowsky Difference can be evaluated as
![\[ S_{A \ominus B}( v ) = S_{A}( v ) - S_{B}( -v ) \]](form_195.png)
This is used in the GJK algorithm to generate the simplex vertices. Thus for every simplex vertex, 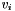 , there exist a corresponding support point,
, there exist a corresponding support point, 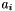 , for
, for 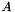 and one,
and one,  , for
, for 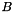 . Thus we have
. Thus we have
![\[ v_i = a_i - b_i \]](form_199.png)
Having found the cloest point, 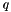 , on the simplex to the origin. Then by the very nature of the simplex we can write
, on the simplex to the origin. Then by the very nature of the simplex we can write 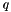 as a convex linear combination. That is
as a convex linear combination. That is
![\[ q = w_1 v_1 + \cdots + w_n v_n \]](form_201.png)
where the 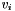 's are the simplex vertices and
's are the simplex vertices and 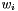 's are scalar weights such that
's are scalar weights such that
![\[ w_1 + \cdots + w_n = 1 \]](form_203.png)
and 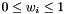 . Thus one immediately recognize the scalar weights as the bary-centric coordinates of q.
. Thus one immediately recognize the scalar weights as the bary-centric coordinates of q.
It is rather straightforward to compute the weights. Once we know them we can use these to obtain the closest points between the two convex sets 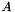 and
and 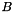 . This is done as follows:
. This is done as follows:
![\[ q = w_1 v_1 + \cdots + w_n v_n = w_1 (a_1 - b_1) + \cdots + w_n (a_n - b_n) \]](form_205.png)
Next re-order
![\[ q = \underbrace{ (w_1 a_1 + \cdots + w_n a_n ) }_{q_a} - \underbrace{ (w_1 b_1 + \cdots + w_n b_n ) }_{q_b} \]](form_206.png)
By convexity of 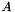 and
and 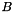 we know
we know

Thus we have found to members of 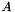 and
and 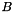 that gives the minimum norm point in the Minikowsky difference. In other words we have found two closest points between
that gives the minimum norm point in the Minikowsky difference. In other words we have found two closest points between 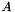 and
and 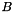 .
.
Member Typedef Documentation
| typedef vector3_type::value_type OpenTissue::gjk::Simplex< vector3_type >::real_type |
| typedef vector3_type::value_traits OpenTissue::gjk::Simplex< vector3_type >::value_traits |
Constructor & Destructor Documentation
| OpenTissue::gjk::Simplex< vector3_type >::Simplex | ( | ) | [inline] |
Member Data Documentation
| vector3_type OpenTissue::gjk::Simplex< vector3_type >::m_a[4] |
The support points from object A corresponding to the simplex vertices.
| vector3_type OpenTissue::gjk::Simplex< vector3_type >::m_b[4] |
The support points from object B corresponding to the simplex vertices.
| int OpenTissue::gjk::Simplex< vector3_type >::m_bitmask |
Bit mask that identifies currently used entries. If (0x0001 & m_bitmask)==1 then it means that the first entry is used. If (0x0002 & m_bitmask)==1 the second is used and if (0x0004 & m_bitmask)==1 then the third one is used and if (0x0008 & m_bitmask)==1 the fourth entry is used. In general if 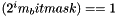 then the i'th array entry is used.
then the i'th array entry is used.
| vector3_type OpenTissue::gjk::Simplex< vector3_type >::m_v[4] |
The simplex vertices.
| real_type OpenTissue::gjk::Simplex< vector3_type >::m_w[4] |
Barycentric coordinates for the closest point on the simplex wrt. the simplex vertices.
The documentation for this class was generated from the following file:
- /home/hauberg/Dokumenter/Capture/humim-tracker-0.1/src/OpenTissue/OpenTissue/collision/gjk/gjk_simplex.h
 1.7.1
1.7.1