PhD Course

Information Geometry in Learning and Optimization

Basic information — Lectures — Practical sessions — Background

Preliminary program

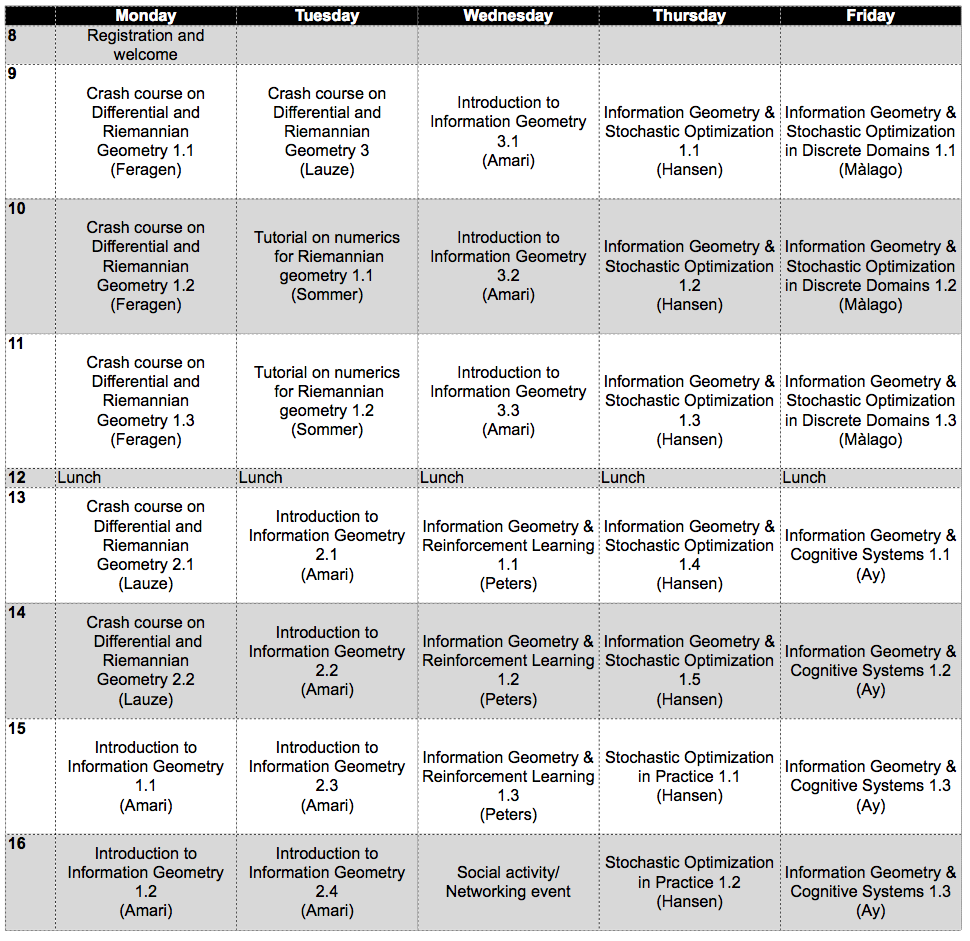
Click here for the preliminary program in pdf format.

Social activities

• Monday: Pizza 17:15. Leaving for Vor Fbyrue Plads metro at 18:20. Guided tour of the old university including dungeons at 19:00.
• Wednesday: Bus to Nyhavn at 15:20, boat tour 16:00-17:00, bus to Nørrebro bryghus (NB) 17:20. Guided tour of NB at 18:00, dinner at NB 19:00.

Lectures overview

Contents of Lectures by Shun-ichi Amari

Click on main headings for slides.

1. Introduction to Information Geometry - without knowledge on differential geometry
   1. Divergence function on a manifold
   2. Flat divergence and dual affine structures with Riemannian metric derived from it
   3. Two types of geodesics and orthogonality
   4. Pythagorean theorem and projection theorem
   5. Examples of dually flat manifold: Manifold of probability distributions (exponential families), positive measures and positive-definite matrices
2. Geometrical Structure Derived from Invariance
   1. Invariance and information monotonicity in manifold of probability distributions
   2. f-divergence : unique invariant divergence
   3. Dual affine connections with Riemannian metric derived from divergence: Tangent space, parallel transports and duality 　　
   4. Alpha-geometry induced from invariant geometry
   5. Geodesics, curvatures and dually flat manifold:
   6. Canonical divergence: KL- and alpha-divergence
3. Applications of Information Geometry to Statistical Inference
   1. Higher-order asymptotic theory of statistical inference – estimation and hypothesis testing
   2. Neyman-Scott problem and semiparametric model
   3. em (EM) algorithm and hidden variables
4. Applications of Information Geometry to Machine Learning
   1. Belief propagation and CCCP algorithm in graphical model
   2. Support vector machine and Riemannian modification of kernels
   3. Bayesian information geometry and geometry of restricted Boltzmann machine: Towards deep learning
   4. Natural gradient learning and its dynamics: singular statistical model and manifold
   5. Clustering with divergence
   6. Sparse signal analysis
   7. Convex optimization

Suggested reading:

• Amari, Shun-Ichi. Natural gradient works efficiently in learning. Neural Computation 10, 2 (1998): 251-276.
• Amari, Shun-ichi, and Hiroshi Nagaoka. Methods of information geometry. Vol. 191. American Mathematical Soc., 2007.

Contents of Lectures by Nihat Ay

1. Differential Equations:
   1. Vector and Covector Fields
   2. Fisher-Shahshahani Metric, Gradient Fields
   3. m- and e-Linearity of Differential Equations
2. Applications to Evolution:
   1. Lotka-Volterra and Replicator Differential Equations
   2. "Fisher's Fundamental Theorem of Natural Selection"
   3. The Hypercycle Model of Eigen and Schuster
3. Applications to Learning:
   1. Information Geometry of Conditional Models
   2. Amari's Natural Gradient Method
   3. Information-Geometric Design of Learning Systems

Contents of Lectures by Nikolaus Hansen

1. A short introduction to continuous optimization
2. Continuous optimization using natural gradients
3. The Covariance Matrix Adaptation Evolution Strategy (CMA-ES)
4. A short introduction into Python (practice session, see also here)
5. A practical approach to continuous optimization using cma.py (practice session)

Suggested reading:

• Hansen, Nikolaus. The CMA Evolution Strategy: A Tutorial, 2011
• Ollivier, Yann, Ludovic Arnold, Anne Auger, and Nikolaus Hansen. Information-Geometric Optimization Algorithms: A Unifying Picture via Invariance Principles. arXiv:1106.3708

Contents of Lectures by Jan Peters

Suggested reading:

• Peters, Jan, and Stefan Schaal. Natural actor critic. Neurocomputing 71, 7-9 (2008):1180-1190

Contents of Luigi Malagò

Stochastic Optimization in Discrete Domains

1. Stochastic Relaxation of Discrete Optimization Problems
2. Information Geometry of Hierarchical Models
3. Stochastic Natural Gradient Descent
4. Graphical Models and Model Selection
5. Examples of Natural Gradient-based Algorithms in Stochastic Optimization

For the gradient flow movie click here.

Suggested reading:

• Amari, Shun-Ichi. Information geometry on hierarchy of probability distributions IEEE Transactions on Information Theory 47, 5 (2001):1701-1711

Contents of Lectures by Aasa Feragen and François Lauze

1. Aasa's lectures
   1. Recap of Differential Calculus
   2. Differential manifolds
   3. Tangent space
   4. Vector fields
   5. Submanifolds of R^n
   6. Riemannian metrics
   7. Invariance of Fisher information metric
   8. If time: Metric geometry view of Riemannian manifolds, their curvature and consequences thereof
2. François's lectures
   1. Riemannian metrics
   2. Gradient, gradient descent, duality
   3. Distances
   4. Connections and Christoffel symbols
   5. Parallelism
   6. Levi-Civita Connections
   7. Geodesics, exponential and log maps
   8. Fréchet Means and Gradient Descent

Suggested reading:

• Sueli I. R. Costa, Sandra A. Santos, and Joao E. Strapasson. Fisher information distance: a geometrical reading. arXiv:1106.3708

Contents of Tutorial by Stefan Sommer

In the tutorial on numerics for Riemannian geometry on Tuesday morning, we will discuss computational representations and numerical solutions of some differential geometry problems. The goal is to be able to implement geodesic equations numerically for simple probability distributions, to visualize the computed geodesics, to compute Riemannian logarithms, and to find mean distributions. We will follow the presentation in the paper Fisher information distance: a geometrical reading from a computational viewpoint.

The tutorial is based on an ipython notebook that is available here. Please click here for details.