Namespaces | |
| namespace | detail |
Classes | |
| class | Projection |
| class | NoProjection |
Functions | |
| template<typename T > | |
| bool | absolute_convergence (T const &f, T const &tolerance) |
| template<typename T > | |
| void | agglomerate_vector (ublas::vector< T > const &x_a, ublas::vector< T > const &x_b, ublas::vector< size_t > const &new2old, ublas::vector< T > &x) |
| template<typename T , typename function_type > | |
| T | armijo_backtracking (function_type const &f, ublas::vector< T > const &nabla_f, ublas::vector< T > const &x, ublas::vector< T > &x_tau, ublas::vector< T > const &dx, T const &relative_tolerance, T const &stagnation_tolerance, T const &alpha, T const &beta, T &f_tau, size_t &status) |
| template<typename T , typename function_type , typename projection_operator > | |
| T | armijo_projected_backtracking (function_type const &f, ublas::vector< T > const &nabla_f, ublas::vector< T > const &x, ublas::vector< T > &x_tau, ublas::vector< T > const &dx, T const &relative_tolerance, T const &stagnation_tolerance, T const &alpha, T const &beta, T &f_tau, size_t &status, projection_operator const &P) |
| template<typename T , typename function_functor , typename gradient_functor > | |
| void | bfgs (function_functor &f, gradient_functor &nabla_f, ublas::compressed_matrix< T > &H, boost::numeric::ublas::vector< T > &x, size_t const &max_iterations, T const &absolute_tolerance, T const &relative_tolerance, T const &stagnation_tolerance, size_t &status, size_t &iteration, T &error, T const &alpha, T const &beta, ublas::vector< T > *profiling=0) |
| template<typename T , typename bound_function_type > | |
| bool | blocking_constraint_search (boost::numeric::ublas::vector< T > const &x, boost::numeric::ublas::vector< T > const &p, bound_function_type const &c, T &tau, size_t &blocking_idx) |
| template<typename bound_functor > | |
| detail::Bound2ConstraintFunctor < typename bound_functor::value_type, bound_functor > | make_constraint_from_lower_bounds (bound_functor const &lower) |
| template<typename bound_functor > | |
| detail::Bound2ConstraintFunctor < typename bound_functor::value_type, bound_functor > | make_constraint_from_upper_bounds (bound_functor const &upper) |
| template<typename T , typename bound_function_type > | |
| void | compute_generalized_minimal_map (ublas::vector< T > const &y, bound_function_type const &l, bound_function_type const &u, ublas::vector< T > const &x, ublas::vector< T > &H) |
| void | compute_index_reordering (ublas::vector< size_t > const &bitmask, ublas::vector< size_t > &old2new, ublas::vector< size_t > &new2old) |
| template<typename T , typename bound_function_type > | |
| void | compute_index_sets (ublas::vector< T > const &y, ublas::vector< T > const &x, bound_function_type const &l, bound_function_type const &u, ublas::vector< size_t > &bitmask, size_t &cnt_active, size_t &cnt_inactive) |
| template<typename T > | |
| T | compute_natural_merit (ublas::vector< T > const &F) |
| std::string | get_error_message (size_t const &error_code) |
| template<typename T > | |
| detail::ConstantVectorBoundFunctor < T > | make_constant_bounds (ublas::vector< T > const &val) |
| template<typename T > | |
| detail::ConstantValueBoundFunctor < T > | make_constant_bounds (T const &value, size_t const &size) |
| template<typename T > | |
| detail::MultibodyDynamicsBoundFunctor < T > | make_lower_mbd_bounds (ublas::vector< size_t > const &pi, ublas::vector< T > const &mu, ublas::vector< T > const &val) |
| template<typename T > | |
| detail::MultibodyDynamicsBoundFunctor < T > | make_upper_mbd_bounds (ublas::vector< size_t > const &pi, ublas::vector< T > const &mu, ublas::vector< T > const &val) |
| template<typename T , typename bound_function_type , typename solver_function_type > | |
| void | non_smooth_newton (ublas::compressed_matrix< T > const &A, ublas::vector< T > const &b, bound_function_type const &l, bound_function_type const &u, boost::numeric::ublas::vector< T > &x, size_t const &max_iterations, T const &absolute_tolerance, T const &relative_tolerance, T const &stagnation_tolerance, size_t &status, size_t &iteration, T &accuracy, T const &alpha, T const &beta, solver_function_type const &sub_system_solver, bool const &use_shur=true, ublas::vector< T > *profiling=0) |
| template<typename T > | |
| void | partition_vector (ublas::vector< T > const &x, ublas::vector< size_t > const &bitmask, ublas::vector< size_t > const &old2new, size_t const &cnt_active, size_t const &cnt_inactive, ublas::vector< T > &x_a, ublas::vector< T > &x_b) |
| template<typename T > | |
| void | perturbation (boost::numeric::ublas::vector< T > &y, T const &lambda, ublas::compressed_matrix< T > const &A, ublas::vector< T > const &b, ublas::compressed_matrix< T > &A_prime, ublas::vector< T > &b_prime) |
| template<typename T > | |
| bool | project (boost::numeric::ublas::vector< T > const &x, boost::numeric::ublas::vector< T > const &l, boost::numeric::ublas::vector< T > const &u, boost::numeric::ublas::vector< T > &new_x) |
| template<typename T > | |
| bool | project (boost::numeric::ublas::vector< T > &x, boost::numeric::ublas::vector< T > const &l, boost::numeric::ublas::vector< T > const &u) |
| template<typename T , typename bound_function_type > | |
| bool | project (boost::numeric::ublas::vector< T > const &x, bound_function_type const &l, bound_function_type const &u, boost::numeric::ublas::vector< T > &new_x) |
| template<typename T , typename bound_function_type > | |
| bool | project (boost::numeric::ublas::vector< T > &x, bound_function_type const &l, bound_function_type const &u) |
| template<typename T , typename function_functor , typename gradient_functor , typename projection_operator > | |
| void | projected_bfgs (function_functor &f, gradient_functor &nabla_f, ublas::compressed_matrix< T > &H, boost::numeric::ublas::vector< T > &x, projection_operator const &P, size_t const &max_iterations, T const &absolute_tolerance, T const &relative_tolerance, T const &stagnation_tolerance, size_t &status, size_t &iteration, T &error, T const &alpha, T const &beta, ublas::vector< T > *profiling=0) |
| template<typename T , typename bound_function_type > | |
| void | projected_gauss_seidel (ublas::compressed_matrix< T > const &A, ublas::vector< T > const &b, bound_function_type const &l, bound_function_type const &u, boost::numeric::ublas::vector< T > &x, size_t const &max_iterations, T const &absolute_tolerance, T const &relative_tolerance, T const &stagnation_tolerance, size_t &status, size_t &iteration, T &accuracy, T &relative_accuracy, ublas::vector< T > *profiling=0) |
| template<typename T , typename function_functor , typename gradient_functor , typename projection_operator > | |
| void | projected_steepest_descent (function_functor &f, gradient_functor &nabla_f, boost::numeric::ublas::vector< T > &x, projection_operator const &P, size_t const &max_iterations, T const &absolute_tolerance, T const &relative_tolerance, T const &stagnation_tolerance, size_t &status, size_t &iteration, T &error, T const &alpha, T const &beta, ublas::vector< T > *profiling=0) |
| template<typename T , typename function_functor , typename gradient_functor , typename projection_operator > | |
| void | projected_steepest_descent (function_functor &f, gradient_functor &nabla_f, boost::numeric::ublas::vector< T > &x, projection_operator const &P, size_t const &max_iterations, T const &absolute_tolerance, T const &relative_tolerance, T const &stagnation_tolerance, size_t &status, size_t &iteration, T &error, T const &tau, ublas::vector< T > *profiling=0) |
| template<typename T > | |
| bool | relative_convergence (T const &f_old, T const &f, T const &tolerance) |
| template<typename T > | |
| bool | stagnation (ublas::vector< T > const &x_old, ublas::vector< T > const &x, T const &tolerance) |
| template<typename T > | |
| bool | stationary_point (ublas::vector< T > const &gradient, T const &tolerance, T &length) |
Variables | |
| size_t const | OK = 0 |
| size_t const | NON_DESCENT_DIRECTION = 1 |
| size_t const | BACKTRACKING_FAILED = 2 |
| size_t const | STAGNATION = 3 |
| size_t const | RELATIVE_CONVERGENCE = 4 |
| size_t const | ABSOLUTE_CONVERGENCE = 5 |
| size_t const | ITERATING = 6 |
| size_t const | DESCEND_DIRECTION_IN_NORMAL_CONE = 7 |
| size_t const | IN_LOWER = 1 |
| size_t const | IN_UPPER = 2 |
| size_t const | IN_ACTIVE = 4 |
Function Documentation
| bool OpenTissue::math::optimization::absolute_convergence | ( | T const & | f, | |
| T const & | tolerance | |||
| ) | [inline] |
Absolute Convergence Test Function.
- Parameters:
-
f The function value at the current iterate. tolerance This argument holds the value used in the absolute stopping criteria. Setting the value to zero will make the test in-effective.
- Returns:
- If the absolute convergence test passes then the return value is true otherwise it is false.
| void OpenTissue::math::optimization::agglomerate_vector | ( | ublas::vector< T > const & | x_a, | |
| ublas::vector< T > const & | x_b, | |||
| ublas::vector< size_t > const & | new2old, | |||
| ublas::vector< T > & | x | |||
| ) | [inline] |
Transfer partitioned vector back to the global un-partitioned system.
- Parameters:
-
x_a A sub-vector that should be transfered into the higher-dimensional vector x. x_b A sub-vector that should be transfered into the higher-dimensional vector x. new2old This vector holds an index permutation of the new indices (in the sub-vectors) to the old indices (in the un-partitioned system). x Upon return this argument holds the agglomerated vector x = pi( x_a, x_b)
| T OpenTissue::math::optimization::armijo_backtracking | ( | function_type const & | f, | |
| ublas::vector< T > const & | nabla_f, | |||
| ublas::vector< T > const & | x, | |||
| ublas::vector< T > & | x_tau, | |||
| ublas::vector< T > const & | dx, | |||
| T const & | relative_tolerance, | |||
| T const & | stagnation_tolerance, | |||
| T const & | alpha, | |||
| T const & | beta, | |||
| T & | f_tau, | |||
| size_t & | status | |||
| ) | [inline] |
Armijo Back-tracking Line-Search.
We can think of f(x) as being a function of the step-length parameter, tau, thus we may write
f( tau ) = f ( x + tau dx )
A first order Taylor approximation around tau=0 yields
f( tau ) ~ f(0) + f'(0) tau
The sufficient decrease conditition (the Armijo condition) is
f( tau ) < f(0) + alpha f'(0) tau
for some alpha in ]0..1]. Observe that
f' = d/d tau f(x + tau dx) = nabla f(x)^T dx
This is nothing more than the directional derivative of f taken at x and in the direction of dx.If we write
gamma = alpha*nabla f(x)^T dx
then we can rephrase the test as follows
f( x + tau dx ) < f(x) + gamma tau
This is the Armijo test used in the un-projected line-search performed by this function.
- Parameters:
-
f The function functor. This is used for computing the value of f(x+tau*dx). nabla_f The value of df/dx at the current iterate. That is the gradient value at the iterate value x. x The current iterate value. x_tau Upon return this argument holds the value of, x + *dx, the new iterate. dx The descent direction along which the line-search is performed. relative_tolerance This argument holds the value used in the relative stopping criteria. Setting the value to zero will make the test in-effective. stagnation_tolerance This argument holds the value used in the stagnation test. It is an upper bound of the infinity-norm of the difference in the x-solution between two iterations. Setting the value to zero will make the test in-effective. alpha Armijo test paramter, should be in the range 0..1, this is the fraction of sufficient decrease that is needed by the line-search method. A good value is often 0.00001; beta The step-length reduction parameter. Everytime the Armijo condition fails then the step length is reduced by this fraction. Usually alpha < beta < 1. A good value is often 0.5; f_tau Upon invokation this argument should hold the value of f(x) upon return the value is set equal to f(x+tau*dx). status Upon return this argument holds the status of the line-search: OK = 0, NON_DESCENT_DIRECTION = 1, BACKTRACKING_FAILED = 2, STAGNATION = 3, RELATIVE_CONVERGENCE = 4.
- Returns:
- The step-length tau.
| T OpenTissue::math::optimization::armijo_projected_backtracking | ( | function_type const & | f, | |
| ublas::vector< T > const & | nabla_f, | |||
| ublas::vector< T > const & | x, | |||
| ublas::vector< T > & | x_tau, | |||
| ublas::vector< T > const & | dx, | |||
| T const & | relative_tolerance, | |||
| T const & | stagnation_tolerance, | |||
| T const & | alpha, | |||
| T const & | beta, | |||
| T & | f_tau, | |||
| size_t & | status, | |||
| projection_operator const & | P | |||
| ) | [inline] |
Armijo Back-tracking Line-Search.
We can think of f(x) as being a function of the step-length parameter, tau, thus we may write
f( tau ) = f ( x + tau dx )
A first order Taylor approximation around tau=0 yields
f( tau ) ~ f(0) + f'(0) tau
The sufficient decrease conditition (the Armijo condition) is
f( tau ) < f(0) + alpha f'(0) tau
for some alpha in ]0..1]. Observe that
f' = d/d tau f(x + tau dx) = nabla f(x)^T dx
This is nothing more than the directional derivative of f taken at x and in the direction of dx.If we write
gamma = alpha*nabla f(x)^T dx
then we can rephrase the test as follows
f( x + tau dx ) < f(x) + gamma tau
This is the Armijo test used in an un-projected line-search. If a projected line-search is done then we can think of x as a function of tau so we write
x(tau) = x + dx*tau
And moving some terms around results in
dx*tau = x(tau) - x
Using this in the original Armijo condition we have
f( x(tau) ) < f(x) + alpha nabla f(x)^T( x(tau) - x)
Next we will keep x(tau) feasible by doing a projection onto a the feasible region
f( P( x(tau) ) ) < f(x) + alpha g(x)^T( P( x(tau) ) - x)
where P is a projection operator, for instance it could be
P( x(tau) ) = max( min( x(tau), u), l )
where u and l would be constant lower and upper bounds for x that is l <= x <= u.
- Parameters:
-
f The function functor. This is used for computing the value of f(x+tau*dx). nabla_f The value of df/dx at the current iterate. That is the gradient value at the iterate value x. x The current iterate value. x_tau Upon return this argument holds the value of, x + *dx, the new iterate. dx The descent direction along which the line-search is performed. relative_tolerance This argument holds the value used in the relative stopping criteria. Setting the value to zero will make the test in-effective. stagnation_tolerance This argument holds the value used in the stagnation test. It is an upper bound of the infinity-norm of the difference in the x-solution between two iterations. Setting the value to zero will make the test in-effective. alpha Armijo test paramter, should be in the range 0..1, this is the fraction of sufficient decrease that is needed by the line-search method. A good value is often 0.00001; beta The step-length reduction parameter. Everytime the Armijo condition fails then the step length is reduced by this fraction. Usually alpha < beta < 1. A good value is often 0.5; f_tau Upon invokation this argument should hold the value of f(x) upon return the value is set equal to f(x+tau*dx). status Upon return this argument holds the status of the line-search: OK = 0, NON_DESCENT_DIRECTION = 1, BACKTRACKING_FAILED = 2, STAGNATION = 3, RELATIVE_CONVERGENCE = 4. P The projection operator, computes x = P(x).
- Returns:
- The step-length tau.
| void OpenTissue::math::optimization::bfgs | ( | function_functor & | f, | |
| gradient_functor & | nabla_f, | |||
| ublas::compressed_matrix< T > & | H, | |||
| boost::numeric::ublas::vector< T > & | x, | |||
| size_t const & | max_iterations, | |||
| T const & | absolute_tolerance, | |||
| T const & | relative_tolerance, | |||
| T const & | stagnation_tolerance, | |||
| size_t & | status, | |||
| size_t & | iteration, | |||
| T & | error, | |||
| T const & | alpha, | |||
| T const & | beta, | |||
| ublas::vector< T > * | profiling = 0 | |||
| ) | [inline] |
The BFGS Method. The BFGS method implemented here is a damped quassi Newton Method. The implementation is a quassi Newton method due to the fact that an approximation is used for the inverse Hessian matrix. The approximation is incrementally updated in each step of the Newton method. An in-exact line-search method is used. The line-search is based on back-tracking until a sufficient decrease condition (The Armijo Condition) is fulfilled. Because the back-tracking may yield a step-length shorter than the pure Newton step length ( 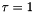 ) the implemented method is a damped Newton method.
) the implemented method is a damped Newton method.
Classically the Newton method is used for unconstrained minimization problems. In the following we will derive the Newton method for this problem. Given a twice continuously differentiable real-valued function,  , we wish to find a minimizer of the function. That is we want to solve the problem
, we wish to find a minimizer of the function. That is we want to solve the problem
![\[ \vec x^* = \min_{\vec x} f(\vec x) \]](form_211.png)
Newtons method is a iterative method and it generates a sequence of iterates,  ,
, 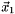 ,
,  ,
,  ,
, 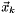 . Hoping that the sequence is converging to the minimizer
. Hoping that the sequence is converging to the minimizer 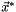 . The
. The 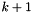 iterate
iterate 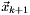 are computed using the update formula
are computed using the update formula
![\[ \vec x_{k+1} = \vec x_{k} + \vec dx_k, \]](form_220.png)
here 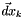 is called the Newton direction of the
is called the Newton direction of the  th step. In the following we will derive the algorithm to find
th step. In the following we will derive the algorithm to find 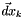 .
.
From Taylors theorem we have
![\[ f(\vec x_k + \vec dx_k) = f(\vec x_k) + \frac{1}{2} \nabla f(\vec x_k) \vec dx_k + \vec dx_k^T \nabla^2 f(\vec x_k ) \vec dx_k + O(\norm{\vec dx_k}^3), *\]](form_223.png)
Next we define a local model of the 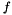 -function, that is
-function, that is
![\[ f(\vec x_k + \vec dx_k) \approx f(\vec x_k) + \nabla f(\vec x_k) \vec dx_k + \frac{1}{2} \vec dx_k^T \nabla^2 f(\vec x_k ) \vec dx_k \equiv m_k(\vec dx_k) *\]](form_225.png)
To find the direction that minimizes the 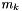 -function we use the first order necessary conditions and solves for
-function we use the first order necessary conditions and solves for 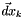 such that the first order derivative of
such that the first order derivative of 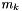 is zero. That is
is zero. That is
![\[ \nabla m_k(\vec dx_k) = 0 \]](form_227.png)
By straight forward differentiation of 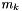 we obtain
we obtain
![\[ \nabla m_k(\vec dx_k) = \nabla f(\vec x_k) + \nabla^2 f(\vec x_k ) \vec dx_k \]](form_228.png)
From all this we obtain the so-called Newton equation
![\[ \nabla^2 f(\vec x_k ) \vec dx_k = - \nabla f(\vec x_k) \]](form_229.png)
and we use this to solve for the Newton direction, 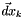 . Provided that
. Provided that 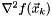 is non-singular and always positive-definite one can ensure the Newton method behaves nicely.
is non-singular and always positive-definite one can ensure the Newton method behaves nicely.
The next extention is to perform a line-search along the Newton direction. That is we want to determine a step-length, 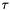 , such that the Newton update,
, such that the Newton update,
![\[ \vec x_{k+1} = \vec x_{k} + \tau \vec dx_k, \]](form_232.png)
results in a sufficient decrease. See the method armijo_backtracking for more details on this.
Lastly instead of computing 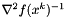 an approximating matrix is used,
an approximating matrix is used,
![\[ H_k \approx \nabla^2 f(x^k)^{-1} \]](form_234.png)
See the method bfgs_update_inverse_hessian for details.
- Parameters:
-
f The function that we seek a minimizer of. nabla_f The gradient of the function that we seek a minizer of. H An initial approximation of the inverse Hessian matrix. This should be a symmetric positive definite matrix. x Upon call this argument holds the current value of the iterate (usefull for warmstarting). Upon return this argument holds solution found by the method. max_iterations This argument holds the value of the maximum allowed iterations. absolute_tolerance This argument holds the value used in the absolute stopping criteria. Setting the value to zero will make the test in-effective. relative_tolerance This argument holds the value used in the relative stopping criteria. Setting the value to zero will make the test in-effective. stagnation_tolerance This argument holds the value used in the stagnation test. It is an upper bound of the infinity-norm of the difference in the x-solution between two iterations. Setting the value to zero will make the test in-effective. status Upon return this argument holds the status of the computation. If status = 0 then iterating has not started due some error If status = 1 then we have not converged to a solution If status = 2 then absolute convergence If status = 3 then the method has stagnated ie. there is not a sufficient change in x between two iterations. If status = 4 then the relative improvement in our merit function is too small between two iterations. If status = 5 then back-tracking failed to produced a step yielding a decrease iteration Upon return this argument holds the number of the iteration when the method exited. error Upon return this argument holds the value of the error of the solution when the method exited. alpha Armijo test paramter, should be in the range 0..1, this is the fraction of sufficient decrease that is needed by the line-search method. A good value is often 0.00001; beta The step-length reduction parameter. Everytime the Armijo condition fails then the step length is reduced by this fraction. Usually alpha < beta < 1. A good value is often 0.5; profiling If this argument is null then profiling is off. If the pointer is valid then profiling is turned on and upon return the vector that is pointed to will hold the values of the merit function at the iterates.
| bool OpenTissue::math::optimization::blocking_constraint_search | ( | boost::numeric::ublas::vector< T > const & | x, | |
| boost::numeric::ublas::vector< T > const & | p, | |||
| bound_function_type const & | c, | |||
| T & | tau, | |||
| size_t & | blocking_idx | |||
| ) | [inline] |
Blocking Constraint Search Function. This function tries to determine whether there are some blocking constraints when trying to update the current iterate x along a specified search direction.
- Parameters:
-
x The current iterate. p The search direction. c The constraint function, we must have c(x) >= 0 tau Upon return this argument holds the step-length that can be taken along the search direction without violating any of the ``linearized'' constraints. blocking_idx Upon return this argument holds the index of one of the blocking constraints (the one with lowest index-value). If no blocking constraint is found then the value is set to one plus the size of the x-vector.
- Returns:
- If the return value is true then a blocking constraint was found.
| void OpenTissue::math::optimization::compute_generalized_minimal_map | ( | ublas::vector< T > const & | y, | |
| bound_function_type const & | l, | |||
| bound_function_type const & | u, | |||
| ublas::vector< T > const & | x, | |||
| ublas::vector< T > & | H | |||
| ) | [inline] |
Non-smooth Generalized Minimal Map Reformulation. Compute value of the generalized minimal map non-smooth reformulation of boxed complementarity problem, also known as a mixed complementarity problem (MCP).
- Parameters:
-
y This vector contains the value of the function y = f(x). l A functor used to retrieve information about the lower bound function. u A functor used to retrieve information about the upper bound function. x The current value of the x-vector. H Upon return this vector holds the value of H_i(x) = min(x_i - l_i, max(x_i - u_i, y_i)).
| void OpenTissue::math::optimization::compute_index_reordering | ( | ublas::vector< size_t > const & | bitmask, | |
| ublas::vector< size_t > & | old2new, | |||
| ublas::vector< size_t > & | new2old | |||
| ) | [inline] |
Compute Reordering of Constraints
- Parameters:
-
bitmask A bitmask vector indicating set membership of the variables. The encoding is as follows:
The i'th value is equal to ``in active'' if bitmask(i) = 4. In terms of complementarity formulations this is true if and only if y(i) (x(i) - lo(i)) && y(i) (x(i) - hi(i))
The i'th value is equal to ``in upper'' if bitmask(i) = 2. In terms of complementarity formulations this is true if and only if y(i) < (x(i) - hi(i))
The i'th value is equal to ``in lower'' if bitmask(i) = 1. In terms of complementarity formulations this is true if and only if y(i) > (x(i) - lo(i))
- Parameters:
-
old2new Upon return this vector holds an index permutation of old indices to new indices. The permutation is such that the first sub-block of the new vector corresponds to active constraints. The second corresponds to lower constraints and the last sub-block corresponds to the upper constraints set. new2old Upon return this vector holds the reversible permuation of old2new.
| void OpenTissue::math::optimization::compute_index_sets | ( | ublas::vector< T > const & | y, | |
| ublas::vector< T > const & | x, | |||
| bound_function_type const & | l, | |||
| bound_function_type const & | u, | |||
| ublas::vector< size_t > & | bitmask, | |||
| size_t & | cnt_active, | |||
| size_t & | cnt_inactive | |||
| ) | [inline] |
Compute index sets.
- Parameters:
-
y This vector contains the value of the function y = f(x). x The current value of the x-vector. l A functor used to retrieve information about the lower bound function. u A functor used to retrieve information about the upper bound function. bitmask A Bitmask, Upon return this vector flags all variables according to their set memberships. The i'th value is equal to ``in active'' if and only if y(i) (x(i) - lo(i)) && y(i) (x(i) - hi(i)) The i'th value is equal to ``in upper'' if and only if y(i) < (x(i) - hi(i)) The i'th value is equal to ``in lower'' if and only if y(i) > (x(i) - lo(i)) cnt_active Upon return this argument holds the total number of variables in the set of active constraints. cnt_inactive Upon return this argument holds the total number of variables in the union of the set of lower and the set of upper constraints.
| T OpenTissue::math::optimization::compute_natural_merit | ( | ublas::vector< T > const & | F | ) | [inline] |
Compute value of natural merit function.
- Parameters:
-
F This argument is expected to hold the vector value of a vector-function.
- Returns:
- Upon return this function returns the value: theta(x) = F(x)^T F(x)/2.
| std::string OpenTissue::math::optimization::get_error_message | ( | size_t const & | error_code | ) | [inline] |
Get Error Message. This function decodes an given error code value into a user friendly and human readable text string. The text string may be convenient for displaying error messages in a log or on screen for an end-user.
- Parameters:
-
error_code The value of an error code.
- Returns:
- A textual and human readable error message string.
| detail::ConstantVectorBoundFunctor<T> OpenTissue::math::optimization::make_constant_bounds | ( | ublas::vector< T > const & | val | ) | [inline] |
Constant Vector Bound Functor Factory Function.
- Parameters:
-
val This vector holds the values of the constant bound function.
- Returns:
- A functor object, representing the bound function.
| detail::ConstantValueBoundFunctor<T> OpenTissue::math::optimization::make_constant_bounds | ( | T const & | value, | |
| size_t const & | size | |||
| ) | [inline] |
Constant Value Bound Functor Factory Function.
- Parameters:
-
value The constant value. size The dimension of the bounds.
- Returns:
- A functor object, representing the bound function.
| detail::Bound2ConstraintFunctor<typename bound_functor::value_type,bound_functor> OpenTissue::math::optimization::make_constraint_from_lower_bounds | ( | bound_functor const & | lower | ) | [inline] |
| detail::Bound2ConstraintFunctor<typename bound_functor::value_type,bound_functor> OpenTissue::math::optimization::make_constraint_from_upper_bounds | ( | bound_functor const & | upper | ) | [inline] |
| detail::MultibodyDynamicsBoundFunctor<T> OpenTissue::math::optimization::make_lower_mbd_bounds | ( | ublas::vector< size_t > const & | pi, | |
| ublas::vector< T > const & | mu, | |||
| ublas::vector< T > const & | val | |||
| ) | [inline] |
Lower Bound Functor Factory Function. This function creates lower bound functor for multibody dynamics formulation.
- Parameters:
-
pi This vector holds the indices of the dependent constraints. For some variables their upper and lower bounds are modelled as a linear dependency on some other variable. That is for the $j$'th variable we might have
lower_j = -mu_j x_i upper_j = mu_j x_i
This vector holds the indices of the depedent variables. That is
pi_j = i
If the j'th entry stores the maximum possible value of the underlying data-type in the vector then it means that there are no dependencies.
- Parameters:
-
mu This vectors holds the values of the linear scaling factor of the dependent constraints. val In case there is no dependent index (pi_j >= n, where n is number of variables) then the constant value stored in this vector is used instead as the bound value.
- Returns:
- A functor object, representing the lower bound function.
| detail::MultibodyDynamicsBoundFunctor<T> OpenTissue::math::optimization::make_upper_mbd_bounds | ( | ublas::vector< size_t > const & | pi, | |
| ublas::vector< T > const & | mu, | |||
| ublas::vector< T > const & | val | |||
| ) | [inline] |
Upper Bound Functor Factory Function. This function creates upper bound functor for multibody dynamics formulation.
- Parameters:
-
pi This vector holds the indices of the dependent constraints. For some variables their upper and lower bounds are modelled as a linear dependency on some other variable. That is for the $j$'th variable we might have
lower_j = -mu_j x_i upper_j = mu_j x_i
This vector holds the indices of the depedent variables. That is
pi_j = i
If the j'th entry stores the maximum possible value of the underlying data-type in the vector then it means that there are no dependencies.
- Parameters:
-
mu This vectors holds the values of the linear scaling factor of the dependent constraints. val In case there is no dependent index (pi_j >= n, where n is number of variables) then the constant value stored in this vector is used instead as the bound value.
- Returns:
- A functor object, representing the upper bound function.
| void OpenTissue::math::optimization::non_smooth_newton | ( | ublas::compressed_matrix< T > const & | A, | |
| ublas::vector< T > const & | b, | |||
| bound_function_type const & | l, | |||
| bound_function_type const & | u, | |||
| boost::numeric::ublas::vector< T > & | x, | |||
| size_t const & | max_iterations, | |||
| T const & | absolute_tolerance, | |||
| T const & | relative_tolerance, | |||
| T const & | stagnation_tolerance, | |||
| size_t & | status, | |||
| size_t & | iteration, | |||
| T & | accuracy, | |||
| T const & | alpha, | |||
| T const & | beta, | |||
| solver_function_type const & | sub_system_solver, | |||
| bool const & | use_shur = true, |
|||
| ublas::vector< T > * | profiling = 0 | |||
| ) | [inline] |
Solve Mixed Complimentarity Problems using a Non-smooth Newton Method.
Given A and b, let y = A x + b and l(x) <= 0 <= u(x). Then this method computes a x-solution to the mixed complimentarity problem defined by:
if y_i > 0 then x_i = l_i(x) if y_i < 0 then x_i = u_i(x) if l_i(x) < x < u_i then y=0
During iterations the nonsmooth reformulation
H(x) = max( x -u(x), min( x-l(x), A x + b ) )
And the merit function
theta(x) = H(x)^T H(x) * 1/2
Is used to measure convergence.
- Parameters:
-
A The coefficient matrix. b The b-vector. l A bound function object type. This object represents the lower bounds and must implement the method with the signature:
T const & () (ublas::vector<T> const & x, size_t const & i) const
- Parameters:
-
u A bound function object type (same type as l-parameter). This object represents the upper bounds. x Upon call this argument holds the current value of the iterate (usefull for warmstarting). Upon return this argument holds solution found by the method. max_iterations This argument holds the value of the maximum allowed iterations. absolute_tolerance This argument holds the value used in the absolute stopping criteria. Setting the value to zero will make the test in-effective. relative_tolerance This argument holds the value used in the relative stopping criteria. Setting the value to zero will make the test in-effective. stagnation_tolerance This argument holds the value used in the stagnation test. It is an upper bound of the infinity-norm of the difference in the x-solution between two iterations. Setting the value to zero will make the test in-effective. status Upon return this argument holds the status of the computation. If status = 0 then iterating has not started due some error If status = 1 then we have not converged to a solution If status = 2 then absolute convergence If status = 3 then the method has stagnated ie. there is not a sufficient change in x between two iterations. If status = 4 then the relative improvement in our merit function is too small between two iterations. If status = 5 then back-tracking failed to produced a step yielding a decrease iteration Upon return this argument holds the number of the iteration when the method exited. accuracy Upon return this argument holds the value of the accuracy of the solution when the method exited. alpha Armijo test paramter, should be in the range 0..1, this is the fraction of sufficient decrease that is needed by the line-search method. A good value is often 0.00001; beta The step-length reduction parameter. Everytime the Armijo condition fails then the step length is reduced by this fraction. Usually alpha < beta < 1. A good value is often 0.5; sub_system_solver The solver that is to be used to solve the linear sub-system. If an iterative solver is used then the relative residual must be less than one in order for the NSN method to achieve local convergence. use_shur A boolean flag used to indicate whether the NSN method should try to use a shur complement to reduce the linear subsystem into a smaller system. It is implicitly assumed that some of the sub-matrices have a particular nice pattern to be easily invertible. Default value is set to true. If set to false then a ``full'' jacobian matrix is used instead, and in this case there is no requirements on the shape of the Jacobian matrix. profiling If this argument is null then profiling is off. If the pointer is valid then profiling is turned on and upon return the vector that is pointed to will hold the values of the merit function at the iterates.
| void OpenTissue::math::optimization::partition_vector | ( | ublas::vector< T > const & | x, | |
| ublas::vector< size_t > const & | bitmask, | |||
| ublas::vector< size_t > const & | old2new, | |||
| size_t const & | cnt_active, | |||
| size_t const & | cnt_inactive, | |||
| ublas::vector< T > & | x_a, | |||
| ublas::vector< T > & | x_b | |||
| ) | [inline] |
Partition vector.
- Parameters:
-
x The value of the vector. bitmask A bitmask, the i'th element is equal to ``active'' value if and only if y(i) (x(i) - lo(i)) && y(i) (x(i) - hi(i)) old2new This vector holds an index permutation of old indices to new indices. The permutation is such that the first sub-block of the new vector corresponds to active constraints. The second corresponds to lower constraints and the last sub-block corresponds to the upper constraints set. cnt_active This argument holds the total number of variables in the set of active constraints. cnt_inactive This argument holds the total number of variables in the union of the set of lower and the set of upper constraints. x_a Upon return this vector holds the values of the sub-block of rhs that corresponds to the active constraints. x_b Upon return this vector holds the values of the sub-block of rhs that corresponds to the inactive constraints.
| void OpenTissue::math::optimization::perturbation | ( | boost::numeric::ublas::vector< T > & | y, | |
| T const & | lambda, | |||
| ublas::compressed_matrix< T > const & | A, | |||
| ublas::vector< T > const & | b, | |||
| ublas::compressed_matrix< T > & | A_prime, | |||
| ublas::vector< T > & | b_prime | |||
| ) | [inline] |
Perturbation Function. In the phd thesis of Billups a pertubed problem is created, by replacing a function f(x) with another function
f(,y,x) = f(x) + (x - y)
where y is termed the center point and >0 is the perturbation value or simply the amount of perturbation.
In the case of the a linear mixed complementarity problem we have f(x) = A x + b, so this implies
f(,y,x) = f(x) + (x - y) = A x + b + (x - y) = (A + I)x + ( b - y)
We thus see that the perturbed problem corresponds to adding a postive value to the diagonal of the coefficient matrix A, and modifying the right-hand-side by subtracting a positive scalar multiple of the center point.
Defining:
A^ = (A + I) b^ = ( b - y)
We see that the perturbed problem is also a affine function of x as is the un-perturbed function.
f(,y,x) = A^ x + b^
This function computes the matrix and rhs-vector of the perturbed problem. Observe that usually A is a symmetric positive semi-definite matrix. Thus A_prime is going to be a symmetric positive definite matrix. In terms of the LCP book by Cottle, Pang, and Stone this is termed a regularization (see page 442).
- Parameters:
-
y The center point. lambda The perturbation value A Original coefficient matrix. b Original right-hand-side vector A_prime Upon return this argument holds the perturbed coefficient matrix. b_prime Upon return this argument holds the perturbed right-hand-side vector.
| bool OpenTissue::math::optimization::project | ( | boost::numeric::ublas::vector< T > const & | x, | |
| boost::numeric::ublas::vector< T > const & | l, | |||
| boost::numeric::ublas::vector< T > const & | u, | |||
| boost::numeric::ublas::vector< T > & | new_x | |||
| ) | [inline] |
Project Operator. Given the iterate x_k, this function performs the projection
x_{k+1} = P(x_k, l, u( )
where l and u are considered to be lower and upper constant bounds of x.
- Parameters:
-
l The lower constant bounds we must have l <= u. u The upper constant bounds we must have l <= u. x This argument holds the current value of the iterate. new_x Upon return this argument holds the projected iterate.
- Returns:
- If a component of x is projected unto the corresponsing component of either l or u, then the return value is true otherwise the return value is false.
| bool OpenTissue::math::optimization::project | ( | boost::numeric::ublas::vector< T > & | x, | |
| boost::numeric::ublas::vector< T > const & | l, | |||
| boost::numeric::ublas::vector< T > const & | u | |||
| ) | [inline] |
Project Operator. This function corresponds to calling the function, project(x,l,u,x);
| bool OpenTissue::math::optimization::project | ( | boost::numeric::ublas::vector< T > const & | x, | |
| bound_function_type const & | l, | |||
| bound_function_type const & | u, | |||
| boost::numeric::ublas::vector< T > & | new_x | |||
| ) | [inline] |
Project Operator. Given the iterate x_k, this function performs the projection
x_{k+1} = P(x_k, l(x_k), u(x_k) )
Since l and u are considered to be functions of x, it may well be that if a component of x is projected then another componenet of x becomes infeasible.
However, if the return value of this function is false then one can be sure that
x_{k+1} = P(x_{k+1}, l(x_{k+1}), u(x_{k+1}) )
Thus one way around an infeasible iterate is to keep on iterating until the function returns false. That is:
while( project( x, l, u , new_x) ) { x = new_x; }
This function do not know anything about the lower and upper bound functions, l and u. That means that in general no guarantee can be given that the above while-loop will terminate with a fix-point iterate x. However, in most cases l and u are simple functions or constants, in which case it should be relatively safe to perform the loop.
- Parameters:
-
l A bound function object type. This object represents the lower bounds and must implement the method with the signature:
T const & () (ublas::vector<T> const & x, size_t const & i) const
- Parameters:
-
u A bound function object type (same type as l-parameter). This object represents the upper bounds. x This argument holds the current value of the iterate. new_x Upon return this argument holds the projected iterate.
- Returns:
- If a component of x is projected unto the corresponsing component of either l or u, then the return value is true otherwise the return value is false.
| bool OpenTissue::math::optimization::project | ( | boost::numeric::ublas::vector< T > & | x, | |
| bound_function_type const & | l, | |||
| bound_function_type const & | u | |||
| ) | [inline] |
Project Operator. This function corresponds to calling the function, project(x,l,u,x);
| void OpenTissue::math::optimization::projected_bfgs | ( | function_functor & | f, | |
| gradient_functor & | nabla_f, | |||
| ublas::compressed_matrix< T > & | H, | |||
| boost::numeric::ublas::vector< T > & | x, | |||
| projection_operator const & | P, | |||
| size_t const & | max_iterations, | |||
| T const & | absolute_tolerance, | |||
| T const & | relative_tolerance, | |||
| T const & | stagnation_tolerance, | |||
| size_t & | status, | |||
| size_t & | iteration, | |||
| T & | error, | |||
| T const & | alpha, | |||
| T const & | beta, | |||
| ublas::vector< T > * | profiling = 0 | |||
| ) | [inline] |
A projected BFGS implemention. See the comments for the bfgs method. This implementation was made to solve problems of the type
![\[ \vec x^* = \min_{\vec x} f(\vec x) \text{s.t.} \vec l \leq x \leq \vec u \]](form_245.png)
It does so by performing a projected line-searh. The idea is to rewrite the constraints as a projection operator,
![\[ P(\vec x) = \min\left( \vec u, \max\left( \vec x, \vec l\right) \right) \]](form_246.png)
See the file optimization_project for examples of such re-writes. Next the projection operator is applied during the line-search to make sure that only feasible iterates are generated. See the method armijo_projected_backtracking for details on the line-search performed.
- Parameters:
-
P The projection operator to be used. Observe that one could specify any projection operator. Even one with variable bounds.
| void OpenTissue::math::optimization::projected_gauss_seidel | ( | ublas::compressed_matrix< T > const & | A, | |
| ublas::vector< T > const & | b, | |||
| bound_function_type const & | l, | |||
| bound_function_type const & | u, | |||
| boost::numeric::ublas::vector< T > & | x, | |||
| size_t const & | max_iterations, | |||
| T const & | absolute_tolerance, | |||
| T const & | relative_tolerance, | |||
| T const & | stagnation_tolerance, | |||
| size_t & | status, | |||
| size_t & | iteration, | |||
| T & | accuracy, | |||
| T & | relative_accuracy, | |||
| ublas::vector< T > * | profiling = 0 | |||
| ) | [inline] |
Project Gauss Seidel Solver for Mixed Complementarity Problems.
Given A and b, let y = A x + b and l(x) <= 0 <= u(x). Then this method computes a x-solution to the mixed complimentarity problem defined by:
if y_i > 0 then x_i = l_i(x) if y_i < 0 then x_i = u_i(x) if l_i(x) < x < u_i then y=0
During iterations the nonsmooth reformulation
H(x) = max( x -u(x), min( x-l(x), A x + b ) )
And the merit function
theta(x) = H(x)^T H(x) * 1/2
Is used to measure convergence.
- Parameters:
-
A The coefficient matrix. b The b-vector. l A bound function object type. This object represents the lower bounds and must implement the method with the signature:
T const & () (ublas::vector<T> const & x, size_t const & i) const
- Parameters:
-
u A bound function object type (same type as l-parameter). This object represents the upper bounds. x Upon call this argument holds the current value of the iterate (usefull for warmstarting). Upon return this argument holds solution found by the method. max_iterations This argument holds the value of the maximum allowed iterations. absolute_tolerance This argument holds the value used in the absolute stopping criteria. Setting the value to zero will make the test in-effective. relative_tolerance This argument holds the value used in the relative stopping criteria. Setting the value to zero will make the test in-effective. stagnation_tolerance This argument holds the value used in the stagnation test. It is an upper bound of the infinity-norm of the difference in the x-solution between two iterations. Setting the value to zero will make the test in-effective. status Upon return this argument holds the status of the computation. If status = 0 then iterating has not started due some error If status = 1 then we have not converged to a solution If status = 2 then absolute convergence If status = 3 then the method has stagnated ie. there is not a sufficient change in x between two iterations. If status = 4 then the relative improvement in our merit function is too small between two iterations. iteration Upon return this argument holds the number of the iteration when the method exited. accuracy Upon return this argument holds the value of the accuracy of the solution when the method exited. relative_accuracy Upon return this argument holds the value of the relative accuracy between the last two iterations of the method. profiling If this argument is null then profiling is off. If the pointer is valid then profiling is turned on and upon return the vector that is pointed to will hold the values of the merit function at the iterates.
| void OpenTissue::math::optimization::projected_steepest_descent | ( | function_functor & | f, | |
| gradient_functor & | nabla_f, | |||
| boost::numeric::ublas::vector< T > & | x, | |||
| projection_operator const & | P, | |||
| size_t const & | max_iterations, | |||
| T const & | absolute_tolerance, | |||
| T const & | relative_tolerance, | |||
| T const & | stagnation_tolerance, | |||
| size_t & | status, | |||
| size_t & | iteration, | |||
| T & | error, | |||
| T const & | tau, | |||
| ublas::vector< T > * | profiling = 0 | |||
| ) | [inline] |
A projected steepest descent method.
In this version no line-search is performed, instead a projected steepest descent direction is used to update the current iterate.
- Parameters:
-
f The function that we seek a minimizer of. nabla_f The gradient of the function that we seek a minizer of. x Upon call this argument holds the current value of the iterate (usefull for warmstarting). Upon return this argument holds solution found by the method. max_iterations This argument holds the value of the maximum allowed iterations. absolute_tolerance This argument holds the value used in the absolute stopping criteria. Setting the value to zero will make the test in-effective. relative_tolerance This argument holds the value used in the relative stopping criteria. Setting the value to zero will make the test in-effective. stagnation_tolerance This argument holds the value used in the stagnation test. It is an upper bound of the infinity-norm of the difference in the x-solution between two iterations. Setting the value to zero will make the test in-effective. status Upon return this argument holds the status of the computation. If status = 0 then iterating has not started due some error If status = 1 then we have not converged to a solution If status = 2 then absolute convergence If status = 3 then the method has stagnated ie. there is not a sufficient change in x between two iterations. If status = 4 then the relative improvement in our merit function is too small between two iterations. If status = 5 then back-tracking failed to produced a step yielding a decrease iteration Upon return this argument holds the number of the iteration when the method exited. error Upon return this argument holds the value of the error of the solution when the method exited. tau The step-size to be used in each iteration. profiling If this argument is null then profiling is off. If the pointer is valid then profiling is turned on and upon return the vector that is pointed to will hold the values of the merit function at the iterates. P The projection operator to be used. Observe that one could specify any projection operator. Even one with variable bounds.
| void OpenTissue::math::optimization::projected_steepest_descent | ( | function_functor & | f, | |
| gradient_functor & | nabla_f, | |||
| boost::numeric::ublas::vector< T > & | x, | |||
| projection_operator const & | P, | |||
| size_t const & | max_iterations, | |||
| T const & | absolute_tolerance, | |||
| T const & | relative_tolerance, | |||
| T const & | stagnation_tolerance, | |||
| size_t & | status, | |||
| size_t & | iteration, | |||
| T & | error, | |||
| T const & | alpha, | |||
| T const & | beta, | |||
| ublas::vector< T > * | profiling = 0 | |||
| ) | [inline] |
A projected steepest descent method.
This implementation was made to solve problems of the type
![\[ \vec x^* = \min_{\vec x} f(\vec x) \text{s.t.} \vec l \leq x \leq \vec u \]](form_245.png)
It does so by peroforming a projected line-searh. The idea is to rewrite the constraints as a projection operator,
![\[ P(\vec x) = \min\left( \vec u, \max\left( \vec x, \vec l\right) \right) \]](form_246.png)
See the file optimization_project for examples of such re-writes. Next the projection operator is applied during the line-search to make sure that only feasible iterates are generated. See the method armijo_projected_backtracking for details on the line-search performed.
- Parameters:
-
f The function that we seek a minimizer of. nabla_f The gradient of the function that we seek a minizer of. x Upon call this argument holds the current value of the iterate (usefull for warmstarting). Upon return this argument holds solution found by the method. max_iterations This argument holds the value of the maximum allowed iterations. absolute_tolerance This argument holds the value used in the absolute stopping criteria. Setting the value to zero will make the test in-effective. relative_tolerance This argument holds the value used in the relative stopping criteria. Setting the value to zero will make the test in-effective. stagnation_tolerance This argument holds the value used in the stagnation test. It is an upper bound of the infinity-norm of the difference in the x-solution between two iterations. Setting the value to zero will make the test in-effective. status Upon return this argument holds the status of the computation. If status = 0 then iterating has not started due some error If status = 1 then we have not converged to a solution If status = 2 then absolute convergence If status = 3 then the method has stagnated ie. there is not a sufficient change in x between two iterations. If status = 4 then the relative improvement in our merit function is too small between two iterations. If status = 5 then back-tracking failed to produced a step yielding a decrease iteration Upon return this argument holds the number of the iteration when the method exited. error Upon return this argument holds the value of the error of the solution when the method exited. alpha Armijo test paramter, should be in the range 0..1, this is the fraction of sufficient decrease that is needed by the line-search method. A good value is often 0.00001; beta The step-length reduction parameter. Everytime the Armijo condition fails then the step length is reduced by this fraction. Usually alpha < beta < 1. A good value is often 0.5; profiling If this argument is null then profiling is off. If the pointer is valid then profiling is turned on and upon return the vector that is pointed to will hold the values of the merit function at the iterates. P The projection operator to be used. Observe that one could specify any projection operator. Even one with variable bounds.
| bool OpenTissue::math::optimization::relative_convergence | ( | T const & | f_old, | |
| T const & | f, | |||
| T const & | tolerance | |||
| ) | [inline] |
Relative Convergence Test Function.
- Parameters:
-
f_old The function value at the previous iterate. f The function value at the current iterate. tolerance This argument holds the value used in the relative stopping criteria. Setting the value to zero will make the test in-effective.
- Returns:
- If the relative convergence test passes then the return value is true otherwise it is false.
| bool OpenTissue::math::optimization::stagnation | ( | ublas::vector< T > const & | x_old, | |
| ublas::vector< T > const & | x, | |||
| T const & | tolerance | |||
| ) | [inline] |
Stagnation Test Function.
- Parameters:
-
x_old The previous iterate value. x The next iterate value. tolerance This argument holds the value used in the stagnation test. It is an upper bound of the infinity-norm of the difference in the x-solution between two iterations. Setting the value to zero will make the test in-effective.
- Returns:
- If stagnation test passes then the return value is true otherwise it is false.
| bool OpenTissue::math::optimization::stationary_point | ( | ublas::vector< T > const & | gradient, | |
| T const & | tolerance, | |||
| T & | length | |||
| ) | [inline] |
Stationary Point Test Function
- Parameters:
-
gradient The current gradient value. If the gradient is zero then we have a stationary point. In this test we simply test if the length of the gradient is close enough to zero within a given user specified tolerance. tolerance This argument holds the value used in the absolute stopping criteria. Setting the value to zero will make the test in-effective. length Upon return this argument holds the value of the length of the gradient.
- Returns:
- If the 2 norm of the gradient is less than the given threshold then the return value is true otherwise it is false.
Variable Documentation
| size_t const OpenTissue::math::optimization::ABSOLUTE_CONVERGENCE = 5 |
Absolute Convergence Test Succeded. This means that the absolute function value has dropped below a given threshold value. Given the current iterate 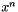 then the test is
then the test is
![\[ f(x^n) < \varepsilon, \]](form_187.png)
where 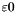 is a user specified test-threshold. In case of minimization the test could also be for a stationary point. The test would then be
is a user specified test-threshold. In case of minimization the test could also be for a stationary point. The test would then be
![\[ | \nabla f(x^n) | < \varepsilon, \]](form_189.png)
| size_t const OpenTissue::math::optimization::BACKTRACKING_FAILED = 2 |
A back-tracking operation failure was detected during some line-search method. This often indicates that the step-length have become too small and no decrease in (merit) function value was obtained.
| size_t const OpenTissue::math::optimization::DESCEND_DIRECTION_IN_NORMAL_CONE = 7 |
Descend Direction is in Normal Cone. This means that the current iterate must be placed on the boundary of the feasible region and that the descend direction is point away from the feasible region in the normal direction. Thus one can not even slide along the boundary of the feasible region in order to minimize ones function value.
In many cases this means that the current iterate is as good as its get (when considering local information only).
| size_t const OpenTissue::math::optimization::IN_ACTIVE = 4 |
In Active Constraint Set Bitmask. Given the general non-linear function, 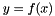 , and the lower and upper bounds:
, and the lower and upper bounds: 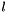 and $$. The non-linear mixed complementarity formulation can be stated as follows
and $$. The non-linear mixed complementarity formulation can be stated as follows
![\[ y_i(x) < 0 \Rightarrow x_i = u_i \]](form_238.png)
![\[ y_i(x) > 0 \Rightarrow x_i = l_i \]](form_239.png)
![\[ y_i(x) = 0 \Rightarrow l_i \leq x_i \leq u_i \]](form_240.png)
The ``in active'' bit is set if and only if 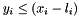 and
and 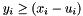 .
.
| size_t const OpenTissue::math::optimization::IN_LOWER = 1 |
In Lower Constraint Set Bitmask. Given the general non-linear function, 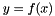 , and the lower and upper bounds:
, and the lower and upper bounds: 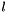 and $$. The non-linear mixed complementarity formulation can be stated as follows
and $$. The non-linear mixed complementarity formulation can be stated as follows
![\[ y_i(x) < 0 \Rightarrow x_i = u_i \]](form_238.png)
![\[ y_i(x) > 0 \Rightarrow x_i = l_i \]](form_239.png)
![\[ y_i(x) = 0 \Rightarrow l_i \leq x_i \leq u_i \]](form_240.png)
The ``in lower'' bit is set if and only if 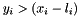 .
.
| size_t const OpenTissue::math::optimization::IN_UPPER = 2 |
In Upper Constraint Set Bitmask. Given the general non-linear function, 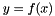 , and the lower and upper bounds:
, and the lower and upper bounds: 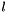 and $$. The non-linear mixed complementarity formulation can be stated as follows
and $$. The non-linear mixed complementarity formulation can be stated as follows
![\[ y_i(x) < 0 \Rightarrow x_i = u_i \]](form_238.png)
![\[ y_i(x) > 0 \Rightarrow x_i = l_i \]](form_239.png)
![\[ y_i(x) = 0 \Rightarrow l_i \leq x_i \leq u_i \]](form_240.png)
The ``in upper'' bit is set if and only if 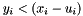 .
.
| size_t const OpenTissue::math::optimization::ITERATING = 6 |
Halted while iterating. This means that somehow for whatever unknown reason the method/function has halted while iterating. In some cases this indicates some internal error. In some cases this may occur if a method/function is being feed a bad (ill-posed or inconsistent) problem to solve.
However in most cases it simply means that the method did not converge within some given maximum number of iterations.
| size_t const OpenTissue::math::optimization::NON_DESCENT_DIRECTION = 1 |
A non descent direction was encountered. This may occur during a line-search method. In which case one expects to perform a line-search along a descent direction.
| size_t const OpenTissue::math::optimization::OK = 0 |
No error occured.
| size_t const OpenTissue::math::optimization::RELATIVE_CONVERGENCE = 4 |
Relative Convergence Test Succeded. This means that the relative improvement in function value has dropped below a given threshold value. Given the current iterate 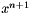 and the previous iterate
and the previous iterate 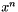 then the test is
then the test is
![\[ \frac{| f(x^{n+1}) - f(x^n) |}{|f(x^n)|} < \varepsilon, \]](form_192.png)
where 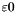 is a user specified test-threshold.
is a user specified test-threshold.
| size_t const OpenTissue::math::optimization::STAGNATION = 3 |
Stagnation occured. Stagnation means that the maximum difference between the components of a new iterate and the old iterate dropped below some small threshold value. Basically it means that the two iterates are nearly the same and no progress have been made by the numerical method used.
 1.7.1
1.7.1