Linear Regression

Background

The general goal of regression is to assign (real-valued) data records to real-valued quantities. For some data records the corresponding quantities are known. These records are used to infer a general function for predicting the correct value of the target variable.

In linear regression, we consider (affine) linear models of the form:

\[y=f(x)=Ax+b\]

If the observed variables x are n dimensional and the dimensionality of the output y is m, then A is a m x n matrix and b a m-dimensional vector call bias, offset or intercept.

Given training data

\[S=\{(x_1, y_1), \dots, (x_l, y_l)\} ,\]

we adapt the model parameters A and b by minimizing the mean squared error

\[\frac{1}{l}\sum_{i=1}^l (y_i - f(x_i))^2.\]

For details see [DMLNa].

Linear Regression in Shark

Toy problem

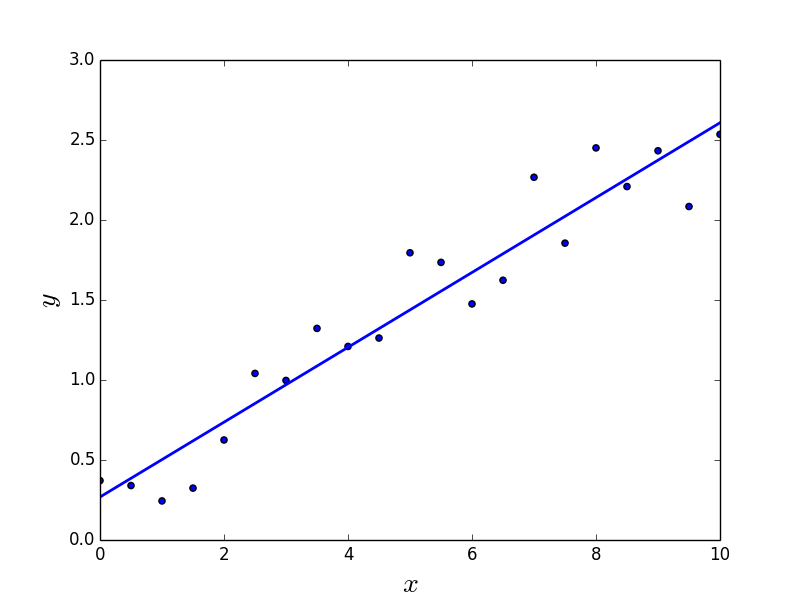
We consider a simple problem with m = n = 1. We are given 21 data points as shown in the following figure.

Reading in the data

Let us consider the example program linearRegressionTutorial.cpp. First, let us read in the data. We assume that the inputs and the labels are stored in two separate files, which are passed as command line arguments. The data considered in this tutorial is in the files regressionInputs.csv and regressionLabels.csv. That is, we invoke the example program by something like:

./linearRegressionTutorial data/regressionInputs.csv data/regressionLabels.csv

The code for reading the data may look like this:

int main(int argc, char **argv) {
        if(argc < 3) {
                cerr << "usage: " << argv[0] << " (file with inputs/independent variables) (file with outputs/dependent variables)" << endl;
                exit(EXIT_FAILURE);
        }
        Data<RealVector> inputs;
        Data<RealVector> labels;
        try {
                importCSV(inputs, argv[1], ' ');
        }
        catch (...) {
                cerr << "unable to read input data from file " <<  argv[1] << endl;
                exit(EXIT_FAILURE);
        }

        try {
                importCSV(labels, argv[2]);
        }
        catch (...) {
                cerr << "unable to read labels from file " <<  argv[2] << endl;
                exit(EXIT_FAILURE);
        }

        RegressionDataset data(inputs, labels);

We read in two Data objects holding the l samples and their labels. Both the input data points and the labels are real vectors and accordingly of the type RealVector, in our simple example 1-dimensional vectors. The function importCSV is used for loading the data from the files, as described in the Importing Data tutorial. The inputs and the labels are combined to a regression data set, which is just another name for LabeledData<RealVector, RealVector>. For importCSV we need:

#include <shark/Data/Csv.h>

And, of course, we assume:

using namespace shark;
using namespace std;

Model and learning algorithm

Now we create the linear model:

LinearModel<> model;

We don’t need to specify the input or output dimensions of the model as the trainer is capable to figure this out by itself. Thus we now only need to declare the algorithm itself to train the model:

LinearRegression trainer;

Given sample data, this trainer finds optimal model parameters of a linear model in the least squares sense as described above. For the model and the trainer we need:

#include <shark/Algorithms/Trainers/LinearRegression.h>

The path reflects the Shark concepts. Of course, the trainer is a AbstractTrainer and every trainer is a (machine learning) Algorithm.

Now we can train the model

trainer.train(model, data);

and inspect the model parameters:

cout << "intercept: " << model.offset() << endl;
cout << "matrix: " << model.matrix() << endl;

The output should look like this:

intercept: [1](0.268685)
matrix: [1,1]((0.2339))

Note the difference between the 1-dimensional intercept vector and the 1x1 matrix A. The model is shown in the following figure.

Evaluating the model

After training the model, we can evaluate it. Let’s apply it to the training data:

Data<RealVector> prediction = model(data.inputs());

We can look at the predictions by cout << prediction<< endl;.

In order to assess the quality of the model, we want to compute the mean-squared error. To this end, we need the proper loss

SquaredLoss<> loss;

from:

#include <shark/ObjectiveFunctions/Loss/SquaredLoss.h>

The squared loss L is defined by L(y,z)=(y-z)². Applied to a set of data, it is averaged over this set and gives the mean squared error as defined above. The squared loss is something to be optimized and accordingly it can be found in the Loss subdirectory of the header directory ObjectiveFunctions.

The line cout << "squared loss: " << loss(data.labels(), prediction) << endl; should write a value close to 0.044.

Full example program

The full example program is linearRegressionTutorial.cpp.

References

[DMLNa]

Christian Igel. Data Mining: Lecture Notes, chapter 3, 2011