Nearest Neighbor Classification
LASSO Regression
Show page sourceK-Means Clustering¶
Background¶
The goal of clustering or segmentation is to assign data points (e.g., records in a database) to groups or clusters. Similar points should be in the same cluster, dissimilar points should be in different clusters. In hard clustering each data point belongs exactly to one group, while in soft clustering a data point can belong to more than one group. The arguably most fundamental segmentation algorithm is k-means clustering, an iterative algorithm in which the number of clusters has to be specified a priori (for details see, e.g., [Bishop2006] or [DMLN]).
K-means Clustering in Shark¶
IN the following, we look at hard clustering using the k-means algorithm.
Sample clustering problem: Old Faithful¶
For this tutorial we need to include the following files:
#include <shark/Data/Csv.h> //load the csv file
#include <shark/Algorithms/Trainers/NormalizeComponentsUnitVariance.h> //normalize
#include <shark/Algorithms/KMeans.h> //k-means algorithm
#include <shark/Models/Clustering/HardClusteringModel.h>//model performing hard clustering of points
First, we load some sample data:
importCSV(data, argv[1], ' ');
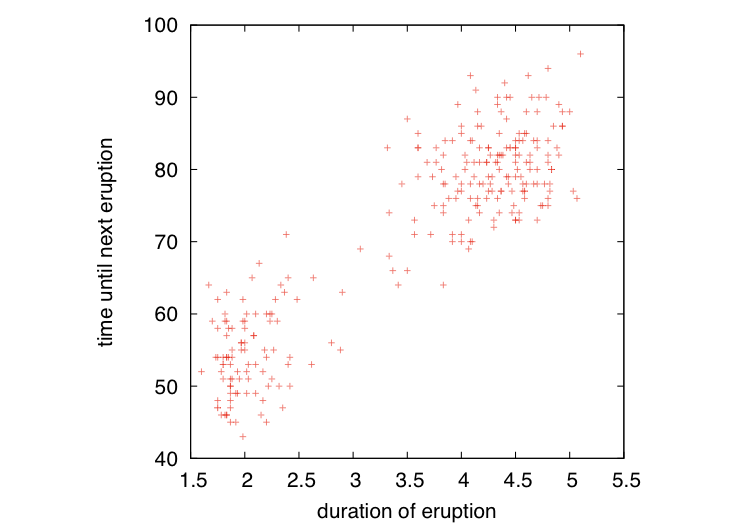
Inspired by [Bishop2006], we consider the Old Faithful data set containing observations from the Old Faithful geyser in Yellowstone National Park, Wyoming, USA:
An entry in the data set contains a measurement of the waiting time until the next eruption of the geyser and the duration of the eruption. The data looks like this:
It is advisable to normalize the data before clustering, see the Normalization of Input Data tutorial:
Normalizer<> normalizer;
NormalizeComponentsUnitVariance<> normalizingTrainer(true);//zero mean
normalizingTrainer.train(normalizer, data);
data = normalizer(data);
Computing the cluster centers¶
Now k-means clustering works like this:
Centroids centroids;
size_t iterations = kMeans(data, 2, centroids);
The cluster centers are stored in the Centroids class. The
number 2 here specifies the number k of clusters. The cluster
centers are updated by the algorithm in an iterative manner. The
function kMeans() returns the number of iterations performed by
the algorithm. An optional parameter can set an upper bound on the
number of iterations.
In general, the result of the clustering depends on the initial centroids in the first iteration of the algorithm. If the centroids are not initialized before they are passed to kMeans(), they are initialized with the first k data points.
The class/cluster centers (centroids) can be assessed as follows:
Data<RealVector> const& c = centroids.centroids();
cout<<c<<std::endl;
Clustering¶
The centroids can now be used to cluster the data. We do a hard clustering by:
HardClusteringModel<RealVector> model(¢roids);
Data<unsigned> clusters = model(data);
The points in the clusters can, for example, be assessed as follows:
for(std::size_t i=0; i != elements; i++) {
if(clusters.element(i))
c1 << data.element(i)(0) << " " << data.element(i)(1) << endl;
else
c2 << data.element(i)(0) << " " << data.element(i)(1) << endl;
}
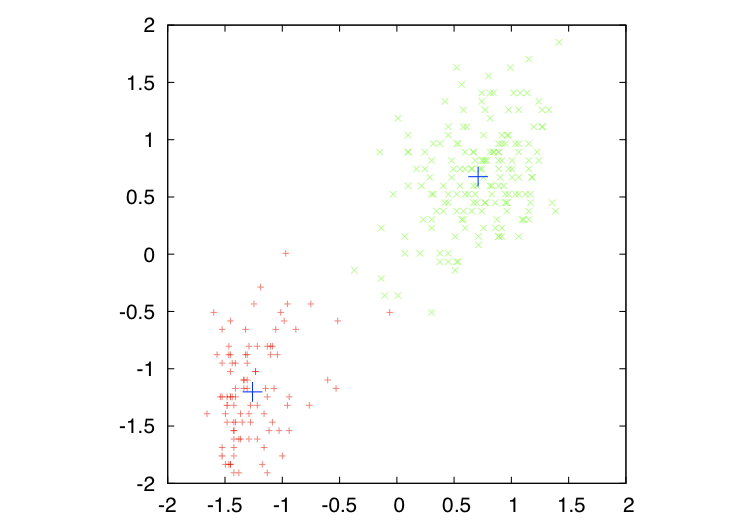
The result of the clustering looks like this (the blue crosses indicate the class centers):
Full example program¶
The full example program is KMeansTutorial.cpp.
