Go to the source code of this file.
Functions | |
| template<typename VectorType > | |
| void | linearRegression (int numPoints, VectorType **points, VectorType *result, int funcOfOthers) |
| template<typename VectorType , typename HyperplaneType > | |
| void | fitHyperplane (int numPoints, VectorType **points, HyperplaneType *result, typename NumTraits< typename VectorType::Scalar >::Real *soundness=0) |
Function Documentation
| void fitHyperplane | ( | int | numPoints, | |
| VectorType ** | points, | |||
| HyperplaneType * | result, | |||
| typename NumTraits< typename VectorType::Scalar >::Real * | soundness = 0 | |||
| ) |
This function is quite similar to linearRegression(), so we refer to the documentation of this function and only list here the differences.
The main difference from linearRegression() is that this function doesn't take a funcOfOthers argument. Instead, it finds a general equation of the form
![\[ r_0 x_0 + \cdots + r_{n-1}x_{n-1} + r_n = 0, \]](form_57.png)
where 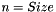 ,
, ![$r_i=retCoefficients[i]$](form_58.png) , and we denote by
, and we denote by 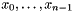 the n coordinates in the n-dimensional space.
the n coordinates in the n-dimensional space.
Thus, the vector retCoefficients has size 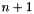 , which is another difference from linearRegression().
, which is another difference from linearRegression().
In practice, this function performs an hyper-plane fit in a total least square sense via the following steps: 1 - center the data to the mean 2 - compute the covariance matrix 3 - pick the eigenvector corresponding to the smallest eigenvalue of the covariance matrix The ratio of the smallest eigenvalue and the second one gives us a hint about the relevance of the solution. This value is optionally returned in soundness.
- See also:
- linearRegression()
| void linearRegression | ( | int | numPoints, | |
| VectorType ** | points, | |||
| VectorType * | result, | |||
| int | funcOfOthers | |||
| ) |
For a set of points, this function tries to express one of the coords as a linear (affine) function of the other coords.
This is best explained by an example. This function works in full generality, for points in a space of arbitrary dimension, and also over the complex numbers, but for this example we will work in dimension 3 over the real numbers (doubles).
So let us work with the following set of 5 points given by their 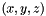 coordinates:
coordinates:
Vector3d points[5]; points[0] = Vector3d( 3.02, 6.89, -4.32 ); points[1] = Vector3d( 2.01, 5.39, -3.79 ); points[2] = Vector3d( 2.41, 6.01, -4.01 ); points[3] = Vector3d( 2.09, 5.55, -3.86 ); points[4] = Vector3d( 2.58, 6.32, -4.10 );
Suppose that we want to express the second coordinate ( 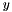 ) as a linear expression in
) as a linear expression in 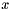 and
and 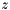 , that is,
, that is,
![\[ y=ax+bz+c \]](form_43.png)
for some constants 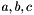 . Thus, we want to find the best possible constants
. Thus, we want to find the best possible constants 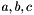 so that the plane of equation
so that the plane of equation 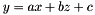 fits best the five above points. To do that, call this function as follows:
fits best the five above points. To do that, call this function as follows:
Vector3d coeffs; // will store the coefficients a, b, c linearRegression( 5, &points, &coeffs, 1 // the coord to express as a function of // the other ones. 0 means x, 1 means y, 2 means z. );
Now the vector coeffs is approximately 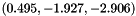 . Thus, we get
. Thus, we get 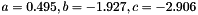 . Let us check for instance how near points[0] is from the plane of equation
. Let us check for instance how near points[0] is from the plane of equation 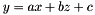 . Looking at the coords of points[0], we see that:
. Looking at the coords of points[0], we see that:
![\[ax+bz+c = 0.495 * 3.02 + (-1.927) * (-4.32) + (-2.906) = 6.91.\]](form_48.png)
On the other hand, we have 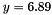 . We see that the values
. We see that the values 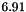 and
and 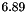 are near, so points[0] is very near the plane of equation
are near, so points[0] is very near the plane of equation 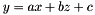 .
.
Let's now describe precisely the parameters:
- Parameters:
-
numPoints the number of points points the array of pointers to the points on which to perform the linear regression result pointer to the vector in which to store the result. This vector must be of the same type and size as the data points. The meaning of its coords is as follows. For brevity, let 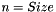 ,
, ![$r_i=result[i]$](form_53.png) , and
, and 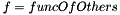 . Denote by
. Denote by 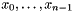 the n coordinates in the n-dimensional space. Then the resulting equation is:
the n coordinates in the n-dimensional space. Then the resulting equation is:
![\[ x_f = r_0 x_0 + \cdots + r_{f-1}x_{f-1} + r_{f+1}x_{f+1} + \cdots + r_{n-1}x_{n-1} + r_n. \]](form_56.png)
funcOfOthers Determines which coord to express as a function of the others. Coords are numbered starting from 0, so that a value of 0 means 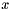 , 1 means
, 1 means 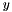 , 2 means
, 2 means 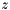 , ...
, ...
- See also:
- fitHyperplane()
 1.7.1
1.7.1